Heat Transfer

1

Fenómenos de Transporte II

Introducción

En primer lugar tenemos que decir que la transferencia de calor es elárea de la ingeniería que estudia los diferentes mecanismos detransferencia de calor.

Definición termodinámica de calor: Es la forma de energía en tránsi to,que se manif iesta debido a una di ferencia de temperaturas.

Nomenclatura.En este curso emplearemos la letra q minúscula para designar el flujode calor.

[W]calor de Flujo :q

y q doble prima, q” para designar el flujo de calor por unidad deárea,

][W/m área de unidadpor calor de Flujo :" 2q

Mecanismos de transferencia de calor.

Existen tres mecanismos básicos de transferencia de calor, ellos son:

• Conducción• Convección• Radiación

Conducción : Se define a la transferencia de calor que ocurri rá através del medio en el cual existe un gradiente de temperaturas.Puede tomar lugar en sól idos, l íquidos y / o gases.

Convección : Se refiere a la transferencia de calor que ocurri rá entreuna superficie y un fluido en movimiento como resul tado de ladi ferencia de temperatura entre la superficie y el f luido.

Radiación : Las superficies emiten energía en forma de ondaselectromagnéticas. A pesar que no exista un medio (vacio) seestablecerá un intercambio de calor por radiación entre dossuperficies a di ferentes temperaturas. Esta característica que tiene la

2

radiación térmica de no necesi tar de medio es precisamente la que ladistingue de los dos mecanismos anteriores.

MedioFluidoen reposoó solido

21 TT >

1T

2T

q

Conducción

1T

2T

Acero

q

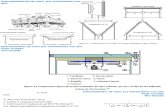
Figura 1.1 Ejemplo de conducción

En la Figura 1.1 se ilustra la si tuación en donde el mecanismo deconducción esta presente, esta corresponde al caso de una paredplana que esta expuesta a dos temperaturas, como consecuencia deesta di ferencia de temperaturas se establecerá un flujo de calor através de la pared. Es importante señalar que si se considera el f lujode calor unidimensional y la conductividad térmica constante, ladistribución de temperaturas en la pared será lineal .

Leyes y ecuaciones que gobiernan los Mecanismos de Transferencia de Calor.

• Ley de Fourier. Conducción• Ecuación de enfriamiento de Newton. Convección• Ley de Stefan-Boltzmann. Radiación

Ley de Fourier.

Es la ley física que describe matemáticamente el mecanismo detransferencia de calor por conducción.

3

xxq

A

Figura 1.2 Ley de Fourier

Con referencia a la figura 1.2, la ley de Fourier establece:

dx

dTkAq x −=

donde:

conducciónpor calor de Flujo :xq

][m al transversárea : 2A

m

K ras temperatude gradiente :

dx

dT

[W/mK] dad,conductivi :k

En la ley de Fourier, la conductividad Térmica, k , es una propiedaddel medio. En general , la conductividad térmica, k , es una propiedadque depende de la temperatura.

A continuación se presenta una Tabla 1.1 representativa de laconductividad térmica de di ferentes materiales.

Tabla 1.1 Conductividad Térmica de diferentes materiales a 300 K

Material mKW /

Plata 427Cobre 400Aluminio 236Hierro 80Madera 0,15

4

Agua 0,60Aire 0,025

En el signo menos que aparece en la ley de Fourier, es unaconsecuencia de satisfacer la segunda Ley de la Termodinámica quepara este caso impone que el f lujo de calor debe darse siempre,desde la región de mayor temperatura hacia la región de menortemperatura.

En la f igura 1.3 se i lustra que si el gradiente de temperaturas esnegativo el flujo de calor, según el sistema de coordenadas señaladodebe ser posi t ivo, y en caso de ser el gradiente de temperaturasposi t ivo, el f lujo de calor debe ser negativo.

T

q

0 <dx

dT

0 >q

x

Figura 1.3 Justificación del signo menos en la Ley de Fourier

T

q

0 >dxdT

0 <q

5

Ecuación de enfriamiento de Newton .

y

sT sT

)(yU )(yT

yqconv

Fluido∞U ∞T

Figura 1.4 Ecuación de enfriamiento de Newton.

Las condiciones de corriente l ibre se suceden en donde los valores

de ∞U y ∞T se hacen independientes de y .

Es importante señalar la naturaleza empírica que tiene la ecuación deNewton, la cual haciendo referencia a la Figura 1.4, se establece losiguiente:

) ( ∞−= TTAhq sconv

donde:

:convq W[ convecciónpor calor de Flujo ]

:h ]/[ convecciónpor calor de ncia transferede ecoeficient 2KmW

] [ pared lay fluido el entre contacto de área: 2mA

6

En la ecuación de Newton, h no es una propiedad termofisica ya quedepende de una gran variedad de factores tanto geométricos comofluidodinámicos.

7

Ley de Stefan- Boltzmann

Cuerpo negro

T

"q

Figura 1.5 Ley de Stefan- Boltzmann

La ley de Stefan- Boltzmann, establece que si un cuerpo se encuentraa una determinada temperatura, este emite calor que vienecuanti f icado por:

4ATqrad σ=

Donde:

][ radiación,por calor de Flujo Wqrad =] [ absoluta, aTemperatur KT =

] /[ 1067,5 Boltzmann,-Stefan de Constante 428 KmW−⋅== σσ

La ley de Stefan-Boltzmann, apl ica a los denominados cuerposnegros, que son aquel los cuerpos que emiten la mayor cantidad decalor posible.En la práctica los cuerpos negros son una ideal ización, en realidadlos cuerpos reales solamente emiten una fracción de la energía queemite un cuerpo negro. A dichos cuerpos se les denominan cuerposgrises.

8

Flujo de calor en cuerpos grises

Figura 1.6 Flujo de calor en cuerpos grises

Para el caso de cuerpos grises la ecuación de Stefan- Boltzmann semodifica, incluyendo la emisividad Térmica, ε , de forma que para uncuerpo gris, el f lujo de calor viene dado por:

4ATqrad εσ=

al)adimension ( Emisividad=ε

La Emisividad depende de la temperatura y el acabado superficial yvaria entre

.10 << ε

A continuación se presenta en la Tabla 1.2 los valores característicosde la emisividad para una temperatura de 300 K

Tabla 1.2 Emisividad de diversos materiales a 300 K

Material ) 300 ( Kε

AluminioPul ido 0,04Anodizado 0,82

AceroPul ido 0,17Oxidado 0,87

Asfal to 0,87 -0,93

Madera 0,82 – 0,92

PinturaNegra 0,98Blanca 0,90Piel 0,95

1

Flujo de calor neto entre cuerpos negros. Para cuantificar el flujo neto de calor entre dos cuerpos negros, se puede realizar usando la siguiente expresión:

)( 42

41 1 TTAq −= σ

2T

1T1A

Figura 1.7 Flujo de calor neto entre cuerpos negros

Flujo de calor neto entre un cuerpo gris y un cuerpo negro Para la situación en la cual el cuerpo 1 es un cuerpo gris y el cuerpo 2 es un cuerpo negro, el flujo de calor, se calcula mediante:

)( 42

4111 TTAq −= εσ

2T

1T21 TT >

Negro1A

1ε

Figura 1.8 Flujo de calor entre un cuerpo gris y un cuerpo negro.

2

Analogía eléctrica para transferencia de calor. Una práctica muy utilizada para la resolución de problemas de transferencia de calor, es la aplicación de la analogía eléctrica, la cual establece una analogía entre las siguientes variables: Electricidad Transferencia de calor Intensidad, i Flujo de calor, q

Voltaje, V Temperatura, T

Ley de Ohm, lec

VI

Re∆=

térR

Tq

∆=

En esencia, la analogía eléctrica consiste en identificar la resistencia térmica, .térmR

1T 2T

q

termR

Figura 1.9 Analogía eléctrica

A continuación se realiza la determinación de la resistencia térmica, asociada a cada mecanismo. Conducción

KA

LTT

L

TTKAq 2121 −− ==

de manera que cR=termR

KA

LRc =

Convección

)( 21 TThAq −=

hARh

1=

3

Radiación )(: 4

24

1 TTAq −εσ

)( 42

41

21

21

TTA

TTTT

q

−−−

=

εσ

)( 42

41

21

TTA

TTRr −

−=εσ

Con frecuencia se habla de un coeficiente de transferencia de calor por radiación, el cual se expresa mediante:

)(

)(

21

42

41

TT

TThr −

−=

σε

Los resultados anteriores se pueden resumir en la Tabla 1.3:

Tabla 1.3 Resistencia Térmica para cada mecanismo

Mecanismo Resistencia

Conducción

KA

L

Convección

hA

1

Radiación

)( 42

41

21

TT

TT

−−

σε

Ejemplo 1.1 Se desea calcular el calor transferido por conducción a través de una placa de vidrio de

conductividad térmica, ][8.0mK

WK = , espesor, L= 1 cm y Área de 122m . Las temperaturas externas e

internas de la placa de vidrio son: CT °= 31 y CT °−= 12 , respectivamente.

Solución

Datos 2m12=A

][8.0Km

WK

°=

CT °= 31

4

0.01mcm 1 ==L

CT °−= 12

)( 21 TTL

KAqk −=

][3840)4(01.0

128.0W

xqk ==

]/[0010417.012 8.0

01.0WK

KA

LRk =

⋅==

1T 2T

q

KAL

== kRKA

L Resistencia por conducción

Figura 1.10 Analogía eléctrica para el ejemplo 1.1

Paredes compuestas Paredes en serie En la practica se presentan paredes compuestas por diversos materiales, en la figura 1.11 se esquematiza una pared compuesta de tres materiales a,b,c dispuestas en serie. En la figura se presenta el circuito eléctrico análogo al problema térmico de las tres paredes conectadas en serie.

1T

aL bL cL

2T

3T

4T

aK bK cK

Figura 1.11 Paredes compuestas conectadas en serie

5

Circuito eléctrico análogo

a ][KA

Lb ][

KA

Lc ][

KA

L1T 4T

2T 3T

Figura 1.12 Circuito eléctrico análogo para paredes compuestas conectadas en serie

1T 2T

kq

keqR

c][b][a][KA

L

KA

L

KA

LRk

eq ++=

Figura 1.13 La resistencia térmica equivalente, keqR , para paredes conectadas

en serie

La resistencia térmica equivalente,keqR , para paredes conectadas en serie, se calcula recordando que cuando

las resistencias se encuentran en serie, la resistencia equivalente es la suma de las resistencias individuales.

c)(b)(a)(

41

KA

L

KA

L

KA

LTT

q++

−=

Paredes compuestas conectadas en paralelo A continuación se ilustra la situación de una pared compuesta formada por dos materiales, a,b que están conectadas en paralelo.

1T

a

b

aa LK .

bb LK .

2T

6

Figura 1.14 Pared compuesta conectada en paralelo

2T1T

aKAL ]/[

bKAL ]/[

1T 2TReq

Figura 1.15 Circuito eléctrico análogo para una pared compuesta conectada en paralelo

La resistencia térmica equivalente se calcula recordando que la resistencia equivalente de resistencia conectadas en paralelo viene dado por:

RbRaq

11

Re

1 +=

RbRa

RbRaq

+= .

Re

ba

ba

KA

L

KA

LKA

L

KA

L

q)()(

).()(Re

+=

q

TTq

Re21−=

Ejemplo 1.2 Los gastos de combustión de un horno son separados del ambiente el cual se encuentra a 25C° , por una pared de ladrillo de 0.15 m. El ladrillo tiene una conductividad de mKWK / 2.1= ( Silica) y una emisividad de 0.8. Bajo condiciones estacionarios se mide la temperatura de la superficie externa la cual es de

100 C° , convección adyacente a la pared esta actuando caracterizada por, KmWh 2 / 20= ¿ Cuál es la temperatura de la superficie interna del ladrillo.?

7

1TCT 1002 =

Ladrillo

Gases deCombustión

convq"

8.0=ε

C 25=∞T

L

K

condq"

Rq"

Kh 2 W/m20=

Figura 1.16 Esquema del ejemplo 1.2

Solución

∞T

1h

condq'

K

L

)( 442

2

∞

∞

−−

TT

TT

σε

1T

radq"

convq"

2T

Figura 1.17 Circuito eléctrico análogo para el ejemplo 1.2 Datos

KT 373 273100 2 =+=

KT 29827325 =+=∞

mL 15,0=

KmWK °= / 2,1

)( área de unidadpor calor de Flujo "2m

W

A

qq =

W

Km

K

LR k

2

1250,02.1

15.0 " ===

)( 05,020

11"

2

W

Km

hR h ===

8

)/

[ 14414,0))298()373((8.0 x10. 67.5

298373

)("

244842

2

mW

K

TT

TTR k =

−−=

−−= −

∞

∞

σε

1T2T

KR" hrR""q

935,2620935,605.0

1

1441.0

1

"

1

"

1

"

1 =+=+===hrhr RRR

]//[ 03712,0" 2mWKR hr =

1T 2T

eqR"

"q

hrkeq RRR """ +=

1621.0" =eqR

22 / 202003712.0

298373

"" mW

R

TTq

hr

=−=−

= ∞

0,1250 . 2020373"".21 +=+= kRqTT

KT 5,6251 =

CT °= 5,3521

)/[1500)( " 22 mWTThq conv =−= ∞

]/[3.520 )(" 2442 mWTTq rad =−= ∞εσ

9

radconvcond qqq """ +=

]/[ 30,2020" 2mWq cond =

Comprobación

30,2020)( 21 =−TTL

K

53,22521 =−TT

5,6251 =T

CT 5,3251 =

1

Ejemplo 1.3. El parabrisas de un automóvi l es desempañado haciendopasar aire a 40 C° sobre su superficie interna, el h asociado a lasuperficie interna es, KmWhi / 30 2= . Bajo condiciones en las cualesla temperatura externa del aire es de -10 C° y su ho= 65 KmW 2/ . ¿Cuales son las temperaturas internas y externas del parabrisas.? Elespesor del parabrisas es de 4 mm.

Figura 1.18 Esquema del problema 1.3

Datos

) vidrio( / 4,1 KmWK °=

oh1

K

L

hi1

oT ,∞ iT ,∞osT , isT ,

Figura 1.19 Circuito eléctrico análogo para el ejemplo 1.3

2o,, / 968

301

4,1004.0

651

)10(4011

" mW

hik

L

ho

TTq i =

++

−−=++

−= ∞∞

vidrio

"q

m 004.0=L

C10- , °=∞ oT

KmWh 20 / 65=

osT ,

CT i °=∞ 40,

KmWhi2/ 30=

isT ,

2

CChi

qTT iis °=−°=−= ∞ 7,7

30

96840

",,

CCho

qTTs °=+°−=+= ∞ 89,4

65

96810

"0,0,

Ejemplo 1.4 Una placa de vidrio a 600 C° es enfriada haciendo pasaraire sobre una superficie tal que el coeficiente de transferencia decalor KmWh 2/ 5= . Para prevenir que el vidrio se rompa se conoce queel gradiente de temperatura no debe exceder de mmC / 15° encualquier punto del vidrio durante el proceso de enfriamiento. Si laconductividad térmica del vidrio es de mKW / 4,1 y la emisividad de lasuperficie es 0,8. ¿ Cuál es la menor temperatura del aire que puedeemplearse en el proceso?

Figura 1.20. Esquema del Ejemplo 1.4

∞T

radq"

radR

convR

1T 2Tcondq"

convq"

1T

2T

C 600

condq"

K 8,0=ε

radq"

convq"

KmWh / 5 2=

∞T

3

Figura 1.21 Circuito eléctrico análogo al Ejemplo 1.4

2/ 21000/1000154,1" mWmmmdx

dTkq cond =⋅⋅==

convradcond qqq """ +=

) ( " 442 ∞−= TTq rad σε

) ( " 2 ∞−= TThq conv

))273600((5) - )273600 (( 10 5,67 8,0 21000 448∞∞

− −+++⋅= TTx

Resolviendo por ensayo y error se tiene finalmente:

) (346 12.618 CT °=∞

Ejemplo 1.5 El factor de enfriamiento debido al viento, el cual esexperimentado en un día frío y con viento esta relacionado con elincremento de la transferencia de calor desde la piel humana a losalrededores. Considere una capa de tejido adiposo de 3 mm deespesor ( ) / W2,0 mKK = y cuya superficie interior esta mantenida auna temperatura de 36 C° . En un día sin viento el coeficiente detransferencia de calor por convección, h , de la superficie externa es25 KmW / 2 , pero con un viento de 30 Km/h el coeficiente h seincrementa a 65 KmW / 2 . En ambos casos la temperatura ambientees de –15 C° .

a.- ¿ Cuál es la relación de pérdida de calor por unidad de áreadesde la piel en un día de calma a un día con viento?

4

b.- ¿ Cuál será la temperatura de la superficie externa de la piel paraun día de calma y para un día con viento?

c.- ¿Qué temperatura debiera tener el aire en un día de calma de talmanera que origine la misma pérdida de calor que un día con vientocon una temperatura del aire de –15 C° y h = 65 KmW / 2 ?.

L

condq"

CTs °= 361,

2,sT

convq"

" " " qqq condconv ==

003,0 =L

C 15- °=∞T

KmWh 20 / 25 =

KmWhv / 65 2=

KmWK / 2,0 2=

∞Th ,0

Figura 1.22 Esquema del Ejemplo 1.5

Solución

1,sT 2,sT ∞T

K

L

h

1

"q

Figura 1.23 Circuito eléctrico análogo para el Ejemplo 1.5

hK

L

TTq s

1

" 1,

+

−= ∞

a.-

5

q” cal ma = 927,27 ) / 25 ( / 20

2 KmWhmW =

q” vi en t o = 1678,48 ) / 56 ( / 22 KmWhmW v =

552,0 "

" =vientoq

calmaq

b.-

calma: CK

LcalmaqTT ss °=−= 1,22 . " 1,2,

015,0 =K

L

viento: C82,10 " 1,2, °=−=K

LvientoqTT ss

c.-

48,1678 "=q

Kmh 20 W/ 25 =

21, / 48,16781

" mW

hK

L

TTq s =

+

−= ∞

92,31 1, =− ∞TTs

C 3,56 °−=∞T

Conclusión

El efecto del viento frío es equivalente incrementar 2,sT en 11,3 C° y

el q en 1,81 veces.

1

Coeficiente global de transferencia de calor, U

Existen ciertos tipos de problemas, principalmente relacionados conintercambiadores de calor, donde es conveniente simplificar el cálculo del calor,esto se realiza incorporando el concepto de coeficiente global de transferencia decalor, U , el cual se relaciona con el calor mediante la siguiente ecuación:

totalTUq ∆= A

donde:

U: Coeficiente global de transferencia de calor, U = [ KmW / 2 ]

Con relación a la analogía eléctrica podríamos señalar que el coeficiente Globalde transferencia de calor se obtiene al reducir todo el circuito eléctrico análogo, auna sola resistencia total, la cual se relaciona con, U, a través de:

AURtotal

1 =

AURtotal

1 =

1T 2T

Figura 1.24 Coeficiente Global de transferencia de calor

A continuación ilustraremos el cálculo del coeficiente global de transferencia decalor, para el Ejemplo 1.5

2,sT

K

L

h

1 ∞T1,sT

2

1

U

2,sT∞T

Figura 1.25 Cálculo del coeficiente global de transferencia de calor para elEjemplo 1.5

) ( " 2, ∞−= TTUq s

∞−=

TT

qU

s 2,

"

Para un día de calma

KmWTT

Us

calma2

2,

calma / 18,18 15)- ( 36

27.927

q" =

−=

−=

∞

Para un día con viento

KmWTT

Us

viento2

2,

viento / 32,91 15)- ( 36

48.1678

q" =

−=

−=

∞

Resistencia de contacto

Aunque se había despreciado hasta ahora, es importante reconocer que ensistemas compuestos con distintos materiales la caída de la temperatura en lainterfaz puede ser apreciable.Esta situación se ilustra en la figura 1.26

3

AT

BTB

A

xq"

x

kaL /

xct q

TBTAR

"

"

−=

Figura 1.26 Resistencia térmica de contacto

En la figura 1.27 se observa una ampliación de la interfaz

BA

Aire

Aire

Aire

Figura 1.27 Resistencia de contacto entre dos paredes

En ella se incorpora ctR ," que es precisamente la resistencia térmica de contacto.

Por supuesto, si ctR ," =0. Se satisface que B TTA =

Desde el punto de vista del cálculo, la presencia de la resistencia térmica decontacto se cuantifica añadiendo una resistencia adicional, tal como se muestra enla figura.

4

A

A

K

LctR ,"

B

B

K

L

La resistencia térmica de contacto, ctR ," , generalmente se determina

experimentalmente.

ctR ," depende en general de

• Presión de contacto• Acabado superficial

A continuación se presenta una tabla donde se muestra valores característicos dela resistencia térmica de contacto.

Tabla 1.2 Resistencia térmica de contacto para (a) Superficies metálicas bajocondiciones de vacío y (b) Interfaz de Aluminio ( rugosidad; 10

nm),25 N/m 10 con diferentes fluidos interfaciales.

Resistencia térmica de contacto, ] /. [ 10x " 2 4, WKmR ct

(a) Interfaz alvacío

(b )Fluido Interfacial

P res ión decon tac to

1002/ mkN

10 .0002/ mkN

A ire 2 ,75

A ce roinoxidab le

6 - 25 0 ,7 - 4 ,0 H e lio 1 ,05

C obre 1 - 10 0 ,1 – 0 ,5 H id rogeno 0 ,720M agnes io 1 ,5 - 3 ,5 0 ,2 - 0 ,4 A ce ite

S ilicona0 ,525

A lum in io 1 ,5 - 5 ,0 0 ,2 - 0 ,4 G lice rina 0 ,265

5

CONDUCCIÓN

Ecuación General de Conducción

Considera el cuerpo sólido mostrado en la figura 2.1

y

zx

) t , z y, x,(T

Figura 2.1 Ecuación de conducción

Con miras a simplificar la demostración de la ecuación de conducciónrealizaremos el análisis, para el caso de dos dimensiones tal como se muestra enla figura 2.2

"q

2

yy

∆+

"q

2

xx

∆+

2

yy

∆−"q

2

xx

∆−"q

y

],[ yx

'''Gq

Figura 2.2 Balance de calor para el caso de dos dimensiones.

6

En balance de calor se han colocado los calores asociados a cada cara delvolumen de control, así como el calor Gq" , Calor generado por unidad de volumen

]m W / [ 3

Este calor generado incorpora la posibilidad de que el cuerpo genera calorinternamente, como puede ocurrir en una reacción química, en un elementoradioactivo, o bien en un conductor eléctrico.

Recordando la Primera ley de la termodinámica, para un sistema cerrado, la cualestablece:

dt

dU

dt

dWqneto =−

y que en ausencia de trabajo e incorporando la convención de signo para laevaluación del calor neto (calor que entra es positivo, calor que sale es negativo),podemos simplificar a:

dt

dUqqq gensaleentra =+−

y evaluando cada término, tenemos:

dt

dUzyxqzxqqzyqq Gy

yy

yx

xx

x )""( )""( '"

2222

=∆∆∆+∆∆−+∆∆− ∆+∆−∆+∆−

recordando que el cambio de energía interna para un sólido se determinamediante:

dt

dTzCyx

dt

dUv∆∆∆= ρ ,

donde Cv, es el calor especifico a volumen constante.

Realizando expansiones en serie de Taylor y reteniendo solamente los términosde primer orden, se tiene para los flujos de calor en las diversas caras.

2

"" "

2

x

x

qqq x

xxx

∆∂

∂−=∆−

2

"" "

2

x

x

qqq x

xxx

∆∂

∂+=∆+

7

2

"" "

2

y

y

qqq y

yyy

∆∂

∂−=∆−

2

"" "

2

y

y

qqq y

yyy

∆∂

∂+=∆

+

sustituyendo las ecuaciones anteriores en el balance de calor, se tiene:

t

TzCyxzyxGqzxy

y

qzyx

x

qv

yx

∂∂∆∆∆=∆∆∆+∆∆∆

∂∂

−+∆∆∆∂

∂− ρ" )

"( )

"(

Empleando la Ley de Fourier para la determinación de los calores, tenemos:

x

Tkq x ∂

∂−= "

y

Tkq y ∂

∂−= "

y sustituyendo finalmente en la Ecuación, y simplificando por zyx ∆∆∆ , se llega a laEcuación General de Conducción para el caso de dos dimensiones, 2-D

t

TCq

y

Tk

yx

Tk

x vG ∂∂=+

∂∂

∂∂+

∂∂

∂∂

''' ) ( ) ( ρ

Interpretación física de cada término de la ecuación de conducción

t

TCq

y

Tk

yx

Tk

x vG ∂∂=+

∂∂

∂∂+

∂∂

∂∂

''' ) ( ) ( ρ

Flujo neto de Flujo neto de Generación Cambiodecalor por unidad calor por unidad de calor por energía internade Área en de Área en la unidad de por unidad dela dirección x dirección y volumen volumen

8

Para la situación en tres dimensiones, 3 –D, podemos escribir la Ecuación deconducción de calor:

t

TC

z

Tk

zy

Tk

yx

Tk

x v ∂∂=+

∂∂

∂∂+

∂∂

∂∂+

∂∂

∂∂

''q' ) ( ) ( ) ( G ρ

ó en notación simbólica:

t

TCqTk vG ∂

∂=+∇∇ ''' ) ( . ρ

Si la conductividad térmica es constante, entonces la ecuación se simplifica a:

t

TCqTk vG ∂

∂=+∇ ''' 2 ρ

A continuación se presenta la Ecuación de Conducción para sistema decoordenadas cilíndricas y esféricas.

Coordenadas cilíndricas

t

TCq

z

Tk

z

Tk

rr

Tkr

rr vG ∂∂=+

∂∂

∂∂+

∂∂

∂∂+

∂∂

∂∂

) ( ) ( 1

) ( 1 ""

2ρ

φφ

φ

x

y

z

r

), , , ( tzrT φ

Figura 2.3 Sistema de coordenadas cilíndricas

Coordenadas esféricas

t

TCq

TSenk

Senr

Tk

Senrr

Tkr

rrG ∂

∂=+∂∂

∂∂+

∂∂

∂∂+

∂∂

∂∂

) ( 1

)( 1

) ( 1

v"'

22222

2ρ

θθ

θθφφθ

9

φ

x

y

z

),, , , ( tzrT θφθ

r

Figura 2.4 Sistema de coordenadas esféricas

Condiciones de bordes y condiciones iniciales

Par poder ser realizada la integración de la ecuación general de conducción, entérminos matemáticos es menester incluir las condiciones iniciales y de borde .En general, por ser la ecuación general de conducción de primer orden en tiempose requiere del establecimiento de una úica condición icicaial.La condición inicial se refiere a la distribución de temperatura que existe en elinstante de tiempo inicial.

Condición Inicial: T(x, y, z, t=0)= Ti(x,y,z)

Para el caso de las condiciones de borde; se observa que en las variablesespaciales (x,y,z), la derivada de mayor orden que aparece en la ecuación generalde conducción es dos; por tanto se requiere el establecimiento de dos condicionesde borde por cada variable espacial. A continuación incluimos un conjunto decondiciones de borde que aparecen con frecuencia en la formulación deproblemas de conducción.

1. Temperatura especificada constante (condicción de Dirichlet)

x

Ts 0 x, Ts T(x) ==

10

2. Flujo de calor especificado constante (condición de Neuman)

x

''sq

0,'' ==− xqdx

dTk s

3. Ambiente convectivo (Robin)

x

h

∞T 0,)( =−=−∞ xdx

dTkTTh

4. Ambiente radiativo

∞T ε

x

0,)( 44 =−=−∞ xdx

dTkTTσε

1

5. Condición de Interfase

LL

x

1 2 Lxdx

dTk

dx

dTk

LxTT

=−=−

==

,

,

22

11

21

Conducción estacionaria sin generación unidimensionalconsiderando, conductividad térmica constante.

La ecuación que gobierna dicha si tuación es la siguiente:

0 2 =∇ T

Placa plana

1T

2Tx

K

L

Figura 2.5 Conducción en una placa plana

2

La ecuación di ferencial a resolver es:

0 2

2

=dx

Td

y sus correspondientes condiciones de borde son:

0,1 == xTT

LxTT == 2

Integrando la ecuación se obtiene:

2 1 CxCT +=

donde las constantes de integración se evalúan haciendo uso de lascondiciones de borde, obteniéndose finalmente, el perfi l detemperatura:

112 Tx

L

TTT +

−=

que comprueba que la distribución de temperatura en una placaplana, es lineal .

La determinación del f lujo de calor se realiza con la ayuda de la leyde Fourier

)( 21 TTL

KA

dx

dTKAq −=−=

que demuestra que la expresión de la resistencia térmica porconducción es:

KA

LPlR =

3

Ci lindro

1R1T 2T

2R

Figura 2.6 Geometría Cilíndrica

La ecuación di ferencial es;

0 ) ( 1 =

dr

dTr

dr

d

r

Con las siguientes condiciones de borde:

11 para T RrT ==

22 para T RrT ==

integrando la ecuación se obtiene

21 ln CrCT +=

y evaluando las constantes, se t iene:

22

2

1

21 )ln()ln(

)( TR

r

R

RTT

rT +−

=

y el f lujo de calor se calcula mediante:

dr

dTrLK

dr

dTKAqr ) 2 ( π−=−=

4

y que evaluando se arriba a:

)ln(2

1

2

21

R

RTT

Lkqr−

= π

que extendiendo la analogía eléctrica para el caso del cil indro setiene que:

Lk

R

R

Rcil π2

)ln(1

2

=

Dicho sea de paso, esta úl t ima expresión es de mucha uti l idadpráctica, cuando se desea aplicar a una tubería, a continuacióni lustraremos con un ejemplo:

Ejemplo 2.1 La Tubería mostrada en la f igura transporta vapor a unacierta Temperatura, 0T , siendo el coeficiente de Transferencia de

calor, ih . El radio interno y externo de la tubería son, 21 y RR ,respectivamente. La tubería posee una conductividad térmica, kt . Latubería esta cubierta con un material aislante, de conductividadtérmica, ka y radio 3R , siendo la temperatura externa del aislante 3T .Esquematice el ci rcui to eléctrico análogo al problema mostrado en laFigura. Suministre una expresión genérica para el flujo de calor enfunción de las variables suministradas.

5

2R

1R

aislanteL

3R

oT

Figura 2.7 Ejemplo 2.1

Solución

El circui to eléctrico análogo se esquematiza a continuación:

El f lujo de calor viene dado por:

kaL

R

R

ktL

R

R

kLRh

To

Tq

i πππ 2

ln

2

ln

2

1

3

2

3

1

2

1

++

−=

Lkt

R

R

⋅⋅π2

)ln(1

2

Lka

R

R

⋅⋅π2

)ln(2

3

0T1T 2T 3T

LRhi 121

π

6

Esfera

1R

2R2T

1T

Figura 2.8 Concha esférica

La ecuación para la concha esférica es:

0) ( 1 22

=dr

dTr

dr

d

r

con las condiciones de borde:

11 para T RrT ==

22 para T RrT ==

al integrar la ecuación se obtiene:

)11

()

11( 2

21

212 Rr

RR

TTTT −

−

−+=

y el f lujo de calor viene expresado por:

21

21

11)(4

RR

TTkqr

−

−=

π

De manera que la resistencia térmica para el caso de la geometríaesférica es:

7

k

RRResf π4

)11

(21

−=

En la Tabla 2.1 se resume las resistencias térmica para cadageometría.

Tabla 2.1Geometría Resistencia Térmica

Placa plana

KA

LRpl =

Cilindro

kL

R

R

Rcil π2

)ln(1

2

=

Esfera

k

RRResf π4

)11

(21

−=

Ejemplo 2.2 Una tubería de 0.20 m. de diámetro, de paredesdelgadas y construida de acero es usada para transportar vaporsaturado a una presión de 20 bar en un cuarto en el cual latemperatura ambiente es de 25 C° y el coeficiente de transferencia decalor por convección en la superficie externa es de 20 KmW 2/ .

a.- ¿Cuál es la pérdida de calor por unidad de longi tud de la tuberíadesnuda? ¿Cuál es la pérdida de calor por unidad de longi tud, si unacapa de 50 mm. de aislante ( mkk W/058.0= ) es agregada a la tubería?El acero y el aislante tienen una emisividad de 0.8

b.- Los costos asociados con la generación de vapor y la instalacióndel aislante son de $ 4/ 910 J y $ 100/m de longi tud de tubería,respectivamente. Si la l inea de vapor es operada 7500 hr/año ¿Cuantos años serán necesarios para pagar la inversión inicial enaislante?

8

1R1T ST

2R

∞T

L

aislante

Figura 2.9 Esquema del Ejemplo

Solución

Datos:

KT 298,15 =∞

468 1 KT = Tablas Termodinámicas

10,01 =R m

kmWh 2/ 20=

mkWKa / 058,0=

a)

El ci rcui to eléctrico para el caso con aislante se presenta en la Figura

∞T

2 2 1

Rh πL

qq

''=

ak

R

R

π2

ln1

2

)(2 442 ∞

∞

−−

TTR

TT

s

s

πσε

9

Figura 2.10 Circuito eléctrico análogo con aislante

∞T

1 2 1

Rh π

L

qq

''=

si TT =

)(2 441 ∞

∞

−−

TTR

TT

i

i

πσε

Figura 2.11 Circuito eléctrico sin aislante

W

mk

RhR conv 0796,0

10.0220

1

2

1'

1

=⋅⋅⋅

=⋅

=ππ

W

mk 1376.0

)15.298486(10.021067.58.0

15.298486' 448 =

−⋅⋅⋅⋅⋅−= − πradR

W

mk

RRR

radcondeq 0504.0)

'

1

'

1(' 1 =+= −

mWq

TTq / 7,3724

Re' 1 =

−= ∞

Con aislante hay que realizar un proceso de ensayo y error queconsiste en proponer un sT inicial , calcular las resistencias, el calor

y f inalmente recalcular sT , inicialmente se propone KTs 480=

WmKak

R

R

R cond / 1126,1 0.058 x x 210.0

15.0ln

2

ln

'1

2

===ππ

0,0941)15.298480 ( 15.0 21067.58.0

15.298480'

448=

−−= − xxxxx

R rad π

0530,015.0 2 20

1

2

1' 2 =

⋅⋅⋅==

ππRhR conv

10

WmKR

RRconv

condeq / 1465,1)"

1

R"

1 ( '' 1

rad

=++= −

mWR

TTq

eq

i / 61,158"

' =−

= ∞

KqRTT condis 304 ' ' =−=

Se repi ten los cálculos con 304=sT

)15.298304( 15.0 2 10 67.5 8.0

15.298304'

448 −−= − xxxxx

R rad π

)305 ( / 4.157 ' ; 1551.1 ' KTmWqR seq ===

Una vez más;

)15.298305( 15.0 2 10 67.5 8.0

15.298 305 ' 448 −

−= − xxxxxR rad π

KTqR srad 303 4,157'2132.0 ' =→=→=

Los cálculos se presentan tabulados en la Tabla 2.2

Tabla 2.2 Resumen de cálculo

Iter ][ KTs ]['W

mKR rad ]['

W

mKR req

] / [ ' mWq ][ KTs

1 480 0.0941 1.1465 158.6 3042 304 0.2143 1.1551 157.4 3053 305 0.2132 1.1550 157.4 305

Por tanto ] /[ 4.157 ' mWq =

11

b) mañoh

s

Año

hx

Jms

J

maño

ahorro./$ 385 3600 7500

10

4$

. )4.1577.3724(

. 9=−=

Periodo de recuperación = ) meses 3,1 ( años 26.0./385$

/100$ =maño

m

1

Espesor crit ico de aislamiento

Con mucha frecuencia se plantea la si tuación de disminuir el flujo decalor, por tal motivo a continuación discuti remos los elementos másimportantes para l levar a feliz termino el diseño y la escogencia delaislante.Para iniciar la discusión comenzaremos presentando el caso deañadir aislante a una pared plana, tal como se muestra en la Figura2.12

1T ∞TA B

ka kb

La

h

Lb

Figura 2.12 Aislamiento de una pared plana

En la Figura 2.12 se muestra una pared plana, material A, al cual sele agrega un material aislante, B. La expresión para el flujo de calorviene dado por:

hAkbA

Lb

kaA

LaTT

q1

1

++

−= ∞

Si la expresión anterior La, Ka, A y h son conocidos se puedeconstruir la gráfica del flujo de calor versus la longi tud del aislante,Lb,. En forma cual i tativa la gráfica luciría de la siguiente forma:

2

Lb

q

Figura 2.13

En el la se observa que en la medida que Lb se incrementa, el f lujo decalor disminuye.

En el caso de que la geometría que deseamos aislar sea de formaci l índrica, tendríamos la siguiente si tuación.

2R

1R

∞T

aislanteL

h

1T

3R

Figura 2.14 Aislamiento de una geometría cilíndrica .

La expresión del f lujo de calor viene dada por:

3

LRhLk

R

R

Lk

R

R

LRh

TTq

ati 3

2

3

1

2

1

0

2

1

2

ln

2

ln

2

1

ππππ+++

−= ∞

Si en la expresión anterior todas las variables se mantienen fi jas aexcepción de 3R se tendría la siguiente gráfica del f lujo de calor en

función del radio del aislante, 3R .

q

3R2R cr

Figura 2.15 espesor critico de aislamiento

En la Figura 2.15 se observa que si la tubería se encuentra desnuda,caracterizada por el hecho que 23 RR = se t iene un determinado flujode calor, si a la tubería desnuda se le agrega un aislante se observaque el f lujo de calor empieza a aumentar, contrario al objetivobuscado, este incremento del f lujo de calor se sucede hasta que elf lujo de calor alcanza un máximo, que se obtiene precisamentecuando el radio del aislante, 3R , coincide con el radio cri tico deaislamiento,

cr , y es precisamente a parti r de valores superiores a cr ,

que el f lujo de calor comenzara a disminuir, tal como se desea.

Según lo antes señalado la determinación del radio cri t ico deaislamiento es de vi tal importancia para realizar un adecuadoaislamiento.

La determinación del radio cri tico de aislamiento se real izareconociendo que la resistencia térmica debe alcanzar un mínimo, osea que:

4

LRhLk

R

R

Lk

R

R

LRhR

atiterm

3

2

3

1

2

1 2

1

2

ln

2

ln

2

1

ππππ+++=

Si en la expresión anterior se mantiene todas las variablesconstantes a excepción de 3R , se obtendrá un mínimo para crR =3

En términos matemáticos se debe cumpl i r que:

03

=dR

dRterm

realizando la derivación antes señalada se tiene:

LhRkaL

RrcR

dR

dRterm23

33

3 2

1

2

1

0)(ππ

−=== , que simpl i f icando se llega a:

h

karc =

Es decir el radio cri tico de aislamiento depende de la conductividadtérmica del material aislante y del coeficiente de transferencia decalor, h,

Para real izar una selección adecuada del aislante se debe veri ficarsiempre que el radio cri tico de aislamiento sea inferior al radio de latubería desnuda.

Ejemplo 2.3 Un aislamiento de baqueli ta es uti l izado en un cable de10 mm. de diámetro. La temperatura superficial del cable es 200 C° ,debido a una corriente eléctrica que se hace pasar por el cable. Elcable esta en un fluido a 25 C° , y el coeficiente de convección es de140 KmW 2/ ¿ Cuál es el radio cri tico asociado con el revestimiento?¿ Cuál es el flujo de calor para el cable sin revestimiento y conrevestimiento de baquel i ta que corresponde al radio cri t ico? ¿ Cuantabaqueli ta debe agregarse para reducir la transferencia de calorasociada con el cable sin revestimiento en 25%?

SoluciónDi = 0.01 m

5

CT °=∞ 25

kmWh 2/ 140 =

cable

baquelitaDatos

Conductividad térmica de la baqueli ta bk = 1,4 kmW 2/

a.- Cálculo del radio cri t ico de aislamiento:

mh

kr bc 01,0

140

4,1 ===

b.- Calculo del calor del cable desnudo:

m

WTTDhq iidesnudo 770)( =−= ∞π

Para el calculo del flujo de calor revestido con el radio de aislamientocri t ico, maxq

m

W

k

r

r

hr

TTq

b

i

c

c

imax 909

2

ln

2

1

=

+

−= ∞

ππ

c.- Cálculo del espesor para reducir el calor en un 25%, es decir a

6

m

W

m

Wq 577 770 75.0 =⋅=

Se debe real izar un proceso de ensayo y error para determinar elradio de aislante, r.

m

W

k

r

r

rh

TTq

b

i

i 577

2

ln

2

1

=

+

−= ∞

ππ

Resolviendo la ecuación anterior, se tiene:

mr 06,0 ≈

por lo tanto el espesor deseado es de:

mrr i 055,0 =−=δ

Conducción estacionaria 1-D con generación

Placa plana

x

TsTs

2L

0'''

2

2

=+k

q

dx

Td g

C.B. (1) TsT = Lx =

7

(2) 0=dx

dT 0=x

Integrando y hallando las constantes se obtiene:

−+=

22'''

12 L

x

k

LqTsT g

La temperatura máxima se alcanza en el centro de la placa y vienedada por:

k

LqTsT

g

2

2'''

máx +=

Mientras que el f lujo de calor, viene dado por:

xAqdx

dTkAq gx

'''=−=

que pone de manifiesto que el flujo de calor sigue una ley l ineal

x

2L

maxq

el cual viene dado por

VqLqAq ggmax'''''' ==

ci l indro

8

r

2R

01

'''

=+

k

q

dr

dTr

dr

d

rg

C.B. (1) TsT = Rr =

(2) 0=dr

dT 0=r

−+=

22'''

14 R

r

k

RqTsT

g

esfera

01

'''2

2=+

k

q

dr

dTr

dr

d

r

g

C.B. (1) TsT = Rr =

(2) 0=dr

dT 0=r

−+=

22'''

16 R

r

k

RqTsT

g

1

Ejemplo. Una placa plana esta compuesta de dos materiales A y B. La

pared del material A t iene una generación de calor 3

6''' 105.1m

wqg ⋅= ,

kA=75 w/mk y LA= 50 mm.. El material B no t iene generación, conKB=150 W/mK y LB=20 mm. . La superficie interna del material A estáperfectamente aislada y la superficie externa del material B se enfríamediante agua con CT o30=∞ y KmWh 2/1000= . Se pide hal lar: (a) elcalor disipado, (b) la temperatura de la interfase y (c) La temperaturamáxima.

AL

A B

BL

aislado CT

KmWh

°==

∞ 30

/1000 2

36''' /105.1

.05.0

/75

mWq

mL

mKWk

g

A

A

⋅=

==

mL

mKWk

B

B

02.0

/150

==

máxT

1T

2T

∞T''gq

B

B

k

L

h

11T 2T ∞T

243

6''''' /105,705,0105,1 mWmm

WLqq Agg ⋅=⋅⋅==

2

KW

m

k

LR

B

Bcond ⋅

⋅== −2

4'' 1033,1

KW

m

hRcond ⋅

⋅== −2

3'' 1011

''''''1 )( gconvcond qRRTT ⋅++= ∞

1151 =T

A

Ag

k

LqTT

2

2'''

1máx

⋅+=

CT °= 140máx

Conductvidad térmica variable, 1-D, 0''' =gq

Análisis alternativo

Considere, el cuerpo mostrado en la f igura. En ella, se da laposibil idad que el área transversal dependa de la posición radial .Dado que se acepta que la conducción de calor es unidimensional yen atención a que no existe generación de calor interna ( 0''' =gq ), se

debe satisfacer que el flujo de calor permanecerá constante.

r1r

2r

q

)(),(),( TKrTrA

3

dr

dTrATKq )()(−=

dTTKrA

drq )(

)(−=

∫∫ −= 2

1

2

1

)()(

T

T

r

r

dTTKrA

drq

Introduciendo, el concepto de Conductividad térmica media, mK

12

2

1)(

TT

dTTKK

T

Tm −

−=∫

)()()( 21

2

1

2

1

TTKdTTKrA

drq

T

T m

r

r

−=−= ∫∫De manera, que el calor puede ser calculado por:

∫

−=

2

1)(

)( 21r

r

m

rA

dr

TTKq

donde es posible identi f icar la resistencia térmica , la cual vieneexpresada por:

m

r

r

K

rA

dr

R∫

=

2

1)(

placa; AK

LR

m

=

cil indro; LK

r

r

K

rLdr

Rmm

r

r

ππ

2

)ln(21

2

2

1 ==∫

4

esfera ; mm

r

r

K

rr

K

r

dr

Rπ

π4

114 21

2

2

1

−

==∫

Como puede adverti rse las expresiones de la resistencia térmica sonsimi lares a las desarrolladas para el caso de conductividadconstante, con la excepción que ahora se introduce el concepto deconductividad térmica media.

5

Aletas de enfriamiento.

A di ferencia de la discusión planteada en la sección anterior, existenmuchas si tuaciones de interés practico en donde el objetivofundamental es incrementar el f lujo de calor. Si recordamos la ley deNewton, por un instante.

)( ∞−= TTAhq S

Podríamos, inferi r que si deseamos incrementar el f lujo de calor,deberíamos incrementar h, la di ferencia de temperaturas, o bien elárea.

Precisamente la razón de colocar aletas de enfriamiento esincrementar el área, a efectos de aumentar la transferencia de calor.

Figura 2.17 Ejemplos de aletas

A continuación real izaremos un anál isis para una aleta. En el análisisse propone que existe estado estacionario y que la distribución detemperaturas es sólo función de la coordenada x,T=T(x)

6

2

xx

q ∆−

2

xx

q ∆−

)( ∞−∆⋅⋅= TTxPhq

x∆

A

oT

L

Figura 2.18 Análisis para una aleta

Considere la aleta mostrada en la Figura 2.18, en dicho esquema semuestra el anál isis por primera ley de termodinámica para el volumende control di ferencial .

El balance de calor establece:

0=− saleentra qq

0

2

2

=−− ∆+

∆−

salexx

xx

qqq

2 2

x

dx

dqqq x

xxx

∆−=∆−

2 2

x

dx

dqqq x

xxx

∆+=∆+

Susti tuyendo las expresiones anteriores en balance de calor se tiene:

7

)( ∞−∆−=∆− TTxPhxdx

dqx

donde

xPdAs ∆=

recordando,

dx

dTkAqx −=

se obtiene la ecuación di ferencial de una aleta:

0)( )( =−− ∞TTPhdx

dTkA

dx

d

Si la conductividad térmica, k, y el área son constantes, la ecuaciónse simpl i f ica a:

0)(2

2

=−− ∞TTkA

hP

dx

Td

Para la ecuación anterior vamos a introducir un cambio de variable

∞−= TTθ

y

kA

hPm =2

En estas nuevas variables la ecuación de la aleta se transforma a :

022

2

=− θθm

dx

d

La solución general de la aleta viene dada por:

mxmx ecec −+= 21θ

Las constantes 2 1 y cc se determinan con imposición adecuada de lascondiciones de borde.

8

Una de las condiciones de borde corresponde al hecho de que latemperatura de la base es 0T , de tal manera que fal ta por especi f icarla condición de borde en el otro extremo de la aleta. Para estasi tuación existen diversos modelos:

• Caso I. Aleta infini ta• Caso II. Extremo aislado• Caso III. Extremo convectivo

Caso I. La aleta se supone que es de longi tud infini ta y que latemperatura en el extremo corresponde a ∞T .

Las condiciones de borde corresponden a:

∞====x

xo

,0

0,

θθθ

lo que determina que la distribución de temperaturas venga dadapor :

mxoe

−= θθ

Caso II. Corresponde a especi f icar que el extremo de la aleta seencuentra aislado térmicamente.

Esta condición de borde tiene como fundamento de que todo el calores disipado por la peri feria de la aleta del tal manera que por elextremo prácticamente no se pierde calor.

Según lo antes señalado las condiciones de borde serian:

0 x, 00 =−== TTθθ

Lxdx

d == ,0θ

Imponiendo las condiciones antes señaladas, a la solución general delas aletas se obtiene la siguiente solución:

9

)( cosh

)]( [ cosh0 mL

xLm −⋅= θθ

Caso III. Esta condición de extremo convectivo es la que mejorrepresenta a la si tuación que efectivamente ocurre en el extremo dela aleta; es decir que el extremo pierde calor por convección. Lascondiciones de borde se escriben para este caso como:

0 x, 00 =−== TTθθ

Lxhdx

dk ==− ,θθ

y la solución; viene expresada por :

) senh()( cosh

)]( senh[)]( [ cosh

0

Lmmk

hmL

xLmmk

hxLm

+

−+−⋅= θθ

1

Flujo de calor disipado por la aleta, aq

Para el caso II, el calor transferido por la aleta puede ser cuantificado mediante:

)( )( 000mLtanhhPkAmLtanmAk

dx

dkAq

xa θθθ ==−= =

Eficiencia de una aleta

Se define la eficiencia de una aleta como:

máxq

qa=η

donde máxq , se refiere al calor máximo que podría transferir la aleta, este calormáximo se establecería en el caso hipotético que toda la aleta se mantuviera a latemperatura de la base, en cuyo caso el calor se calcularía, mediante:

)( 0máx ∞−= TTPLhq

De manera que sustituyendo la expresión anterior en la definición de eficiencia seobtiene finalmente:

mL

mLtanh )(=η

En la práctica las aletas pierden calor por el extremo, para contabilizar esa pérdidade calor Jakob, recomienda utilizar las expresiones deducidas para una aleta conextremo aislado pero realizando una corrección a la longitud de la aleta, que vienedada por:

P

ALLc +=

2

Demostración de la aproximación de Jakob

∞Th,

∞Th, ∞Th,

aislada

∞Th, L*

L

ET

ET

La esencia de la aproximación de Jakob consiste en determinar el incremento delongitud de la aleta de suerte tal que el calor que pierde la aleta por el extremo seaequivalente al calor que se transfiere por la periferia de la porción de aletaagregada. La aproximación estriba en suponer que dado que está adición delongitud es pequeña, es plausible decir que la temperatura de esta porción es iguala la temperatura del extremo de la aleta original. En consecuencia , se puedeescribir la siguiente equivalencia:

)()(* *∞∞ −=−= TThATThPLq EE

que al simplificar nos queda : P

AL =*

Con la ayuda de esta aproximación, la cuantificación de la eficiencia de una aletaque pierde calor por convección, puede ser cuantificada mediante:

)(

))(tanh(

P

ALm

P

ALm

+

+=η

Ejemplo 2.4 Determine la transferencia de calor desde la aleta rectangularmostrada en la figura. El extremo de la aleta pierde calor por convección. La aletatiene una conductividad térmica de 150 mKW / . La temperatura de la base es de100 C° y el fluido que circunda a la aleta se encuentra a 20 C° . El coeficiente detransferencia de calor por convección, h, es 30 KmW 2/ .

3

0.4 m

k

0.20 m

0.02 m

∞Th,

CT °=1000

Figura 2.19 Esquema del Ejemplo 2.4

Solución

2095,0 04,080,0

02,0 .40,020,0 =

++=+=

P

ALLc

5826,4==kA

hPm

96.0=cmL

775,0)( ==

mL

mLtanhη

WTThPLq c 35,422)80.(2095,0.84,0.30)( 0máx ==−= ∞

Wqqa 32735,422 .775,0 máx === η

La eficiencia de diversos de aletas se presenta a continuación:

4

2/12/3 )/( pc kAhL

Eficiencia global de un grupo de aleta

Ab: área de la base expuesta al fluidoAf: área superficial de una sola aletaAt: área total incluyendo el área de la base y toda la superficie aleteada, At=Ab+NAf

N: Número total de aletas

q

5

Se define la eficiencia global de un grupo de aletas como:

)1(1 ft

fo A

NAηη −−=

( ) ( )

[( ) ]( ) [ (1 )]( )

[1 (1 )]( ) ( )

t b f b b f f b

t f f f b t f f b

ft f b O t b

t

q q Nq hA T T N hA T T

h A NA N A T T h A NA T T

NAhA T T hA T T

A

ηη η

η η

∞ ∞

∞ ∞

∞ ∞

= + = − + −

= − + − = − − −

= − − − = −

1

La importancia de la eficiencia global es que permite determinar elcalor total transferido por un arreglo de aletas.

Adicionalmente, podemos identi f icar una resistencia térmica asociadaa la presencia de un grupo de aletas.

tohAR

η1=

Ejemplo 2.5 En la f igura se muestra un tubo aleteado (aletasanulares) de diámetro externo, De=16 mm , el diámetro de las aletases, df= 44 mm. Las aletas son fabricadas de aluminio, W/mK178=mK .

El espesor de cada aleta es mmt f 5.0= . El número de aletas por

metro es, N= 395. La temperatura externa, C 50°=∞T , mientras que el

coeficiente convectivo, Khf2 W/m65,43= . La temperatura de la

superficie del tubo es de , C 35°=sT . Para esta configuración, se pidedeterminar: (a) el calor transferido (por unidad de longi tud) por eltubo sin aletas, (b) la eficiencia de una aleta, (c) la eficiencia delgrupo de aletas, (d) el calor transferido (por unidad de longi tud) porel tubo con aletas, (e) La razón entre el calor con aleta y el calor sinaleta.

Di

dfDe

tf

Lf

Esquema del ejemplo 2.5

Solución

(a) W/m32,9135)50(101665,43)(' 3 =−⋅⋅⋅=−= −∞ ππ sef TTDhq

2

(b) Para el cálculo de la eficiencia de la aleta anular, se ha preferidoemplear la expresión aproximada recomendada por Shah1, ensusti tución de la información gráfica.

0.52 f

em

hm

K tf

⋅ = ⋅

*

exp(0.13 1.3863)*

2

e e

fe f

f

m le e

tl l

dr

De

m l r −

= +

=

Φ =

( ) ( )( )

0.445*

0.445*

para 0.6+2.257 r

tanh( ) para 0.6+2.257 r

b

e ea m lη

η

−−

−

= Φ ≥

Φ= Φ ≤Φ

que al susti tuir por los valores numéricos, se t iene:

0.5

3

2*43.6531.27

178.5*0.5*10me −

= = 4

3 35 1014 10 14.25 10

2el−

− −⋅= ⋅ + = ⋅

3*

3

44 102.75

16 10r

−

−⋅= =⋅

33 exp(0.13 31.28 14.25 10 1.3863)31.28 14.25 10 2.75 0.5827−− ⋅ ⋅ ⋅ −Φ = ⋅ ⋅ ⋅ =

tanh(0.5827)=0.900 para 2.038

0.5827η = Φ ≤

(c) Debemos por empezar determinanado las áreas

Ab: área de la base expuesta al f luidoAf: área superficial de una sola aleta

1 Shah Ramesh, “Compact Heat Exchangers” en The CRC Handbook of Thermal Engineering,editor en chief, Frank Kreith, CRC Press, 2000.

3

At: área total incluyendo el área de la base y toda la superficiealeteada, At=Ab+NAf

2353

43-23-23-22ff

m 1070.2109115.610639.2

1051044))10(16)10((444

2)(d4

2A

−−−

−

⋅=⋅+⋅=

=⋅⋅⋅⋅+⋅−⋅⋅=⋅⋅+−⋅= ππππffe tdD

22

324-3-3

10033.4

10927.910026.51051016395)1)(1016()1(

m

tDNDA feeb

−

−−−

⋅=

⋅−⋅=⋅⋅⋅⋅⋅−⋅=⋅−⋅= ππππ

232 11.11070.239510033.4 mNAAA fbt =⋅⋅+⋅=+= −−

904.0)90.01(962.01)90.01(11.1

1070.23951)1(1

3

=−⋅−=−⋅⋅−=−−=−

ft

fo

A

NAηη

(d) mTTAhq Stfoaletacon / W7.656)3550(11.165.43904.0)(' =−⋅⋅⋅=−= ∞η

(e) 95.1991.32

7.656

' ==q

q aletacon

Quiz Sorpresa : Problema 3.124 Libro de Incropera.

Métodos Numéricos

Conducción Unidimensional

• Método de los volúmenes fini tos de control (Patankar, 1980)

Ecuación General

0)(1 =++ cp

nn STS

dr

dTkr

dr

d

r

donde

=esfericas

scilindrica

scartesiana

n

2

1

0

Se escribe la ecuación de esa manera para dar la posibil idad que)(Tkk = y cp STS + , se denomina el término de fuente que involucra a

cualquier término distinto del conductivo.

Ej. Si existe generación interna constante de calor; se tendría''',0 gcP qSS == . Otro ejemplo sería, en la si tuación de modelar una

aleta; en cuyo caso; )( ∞−−=+ TTA

hPSTS cp . En este caso es fáci l

identi ficar que A

hPSp −= y ∞= T

A

hPSc .

(1)La metodología se inicia realizando la discretización del dominio,(2) paso seguido se procede a identi ficar al nodo que caracterizará acada subdominio (volumen fini to de control). Este nodo se encuentraen el centro geométrico del dominio.

P EW

r∆

+∆r−∆r

rw e

Se multiplica la ecuación general por drr n y se integra sobre elvolumen de control P, mostrado en el esquema

( ) 0=++

∫∫ drrSTSdr

dr

dTkr

dr

d ne

w cPne

w

ww

nw

ee

ne

ne

w dr

dTkr

dr

dTkrdr

dr

dTkr

dr

d −=

∫

+∆−≈r

TT

dr

dT PE

e

; r

TT

dr

dT WP

w ∆−

≈

( ) rrSTSdrrSTS nPcPP

ne

w cPP ∆+=+∫ )(

Susti tuyendo las expresiones anteriores; es posible rescribir laecuación discretizada como:

bTaTaTa WWEEPP ++=

donde:

rrSb

rrSaaa

r

kra

r

kra

nPC

nPPWEP

wn

wW

en

eE

∆=

∆−+=∆

=

∆=

−

+

Ejemplo: Empleando tres volúmenes fini tos de control , uni formementeespaciados. Hallar la distribución de temperaturas en una aleta desección rectangular constante con extremo aislado. Compare susresul tados con la solución exacta del problema. Adicionalmente,calcule la eficiencia de la aleta dictada por la solución numérica.Considere para sus cálculos: 1=== oLm θ

Solución:

La ecuación di ferencial a resolver corresponde a:

02

2

=−θθdx

d

1,0

0,1

==

==

xdx

d

x

θθ

Es posible veri ficar que la ecuación generalizada, se reduce a laecuación de la aleta, si se selecciona el siguiente conjunto devariables: 0;1;1;, =−=== CP SSkTθ .

1

3

1

3

1

3

1

1 2 30 4

Cálculo de los coeficientes de influencia:

Volumen de control 1

03

28

3

136

6

6

11

3

3

11

1

1

1

=

=++=

==

==

b

a

a

a

P

W

E

de manera que la ecuación para este volumen de control se puedeescribir como:

021 633

28 θθθ +=


03

19

3

133

3

3

11

3

3

11

2

2

2

=

=++=

==

==

b

a

a

a

P

W

E

312 333

19 θθθ +=


03

28

3

136

3

3

11

6

6

11

3

3

3

=

=++=

==

==

b

a

a

a

P

W

E

243 363

28 θθθ +=

La el iminación de las temperaturas se real iza mediante la imposiciónde las condiciones de borde ,1=oθ y

0

6

134 =

−≈ θθθ

dx

d

La úl t ima ecuación determina que 34 θθ = ; real izando la susti tucióncorrespondiente en la ecuación del volumen de control 3, estaecuación se reduce a:

23 33

10 θθ =

En resumen; el sistema de ecuaciones puede ser escri to en formamatricial mediante:

−=

−−

−

0

0

6

3/1030

33/193

033/28

3

2

1

θθθ

cuya solución es:

8751,01 =θ7225,02 =θ6503,03 =θ

A continuación se presenta una tabla, en la cual se compara con lasolución exacta del problema:

x numérico exacta Error(%)

0 1 1 01/6 0,8751 0,8864 1,30,5 0,7225 0,7308 1,15/6 0,6503 0,6570 1,0

1 0,6503 0,6480 0,4

Solución exacta: )1cosh(

)1cosh( x−=θ

Como puede observarse de los errores que se encuentrantabulados. La solución numérica compara muy bien con la soluciónanalít ica. Este comentario crece en valor cuando se destaca quesolamente se emplearon tres (3) volúmenes fini tos de control paraobtener la solución.

Cálculo numérico de la eficiencia de la aleta

00 ==

−=−=xx

fdx

dkA

dx

dTkAq

θ

omáx hPLq θ=

002

0

1

==

−=−=xxo dx

d

Lmdx

d

hPL

kA θθ

θθ

η

que al susti tuir por valores numéricos

7494.0

6

118751,0

6

101

0

−=−=−

==

θθθxdx

d

7494,0=η

El valor exacto puede ser obtenido al evaluar:

7544,01

)1tanh()tanh(===

mL

mLη ; de manera que el error asociado al cálculo

numérico de la eficiencia es de 0,95 %.

Conducción estacionaria en dos dimensiones

Hasta ahora hemos esbozado las principales soluciones para el casode conducción estacionaria en una dimensión. La incorporación deuna segunda dimensión determina que para el caso más senci l lo; esdecir contemplando conductividad térmica constante y ausencia degeneración de calor. La ecuación a resolver en el caso decoordenadas cartesianas, corresponde a la ecuación de Laplace:

02

2

2

22 =

∂∂+

∂∂=∇

X

T

X

TT

En general lo método para acometer la solución de esta ecuacióndiferencial , los podemos distinguir entre métodos analít icos ymétodos numéricos. Dentro de los métodos analít icos, podemosmencionar: el método de separación de variables y análisis deFourier , t ransformada de Laplace , entre otros. Las metodologíasnuméricas más empleadas corresponden al método de lasdiferencias f initas , el método de los volúmenes f initos de controly el método de los elementos f initos .

Invi tamos al lector, a revisar el material que aparece en el l ibro detexto relativo a las metodologías analít icas.

A continuación, real izaremos la presentación del método de losvolúmenes fini tos de control en 2-D.

Método de los volúmenes f initos de control en 2-D.

Ecuación:

0=++

∂∂+

∂∂

cp STSdy

dTk

ydx

dTk

x

P

N

S

EW

y

xx∆

+∆x −∆x

y∆+∆y

−∆y

multiplicando la ecuación por el di ferencial de área y procediendo aintegrar sobre el volumen fini to e control mostrado en la f igura.

( )∫ ∫∫ ∫∫ ∫ =++

∂∂

∂∂+

∂∂

∂∂ e

w

n

scp

e

w

n

s

n

s

e

w

dydxSTSdydxy

Tk

ydxdy

x

Tk

x0

La discretización se prosigue de la manera siguiente, empezaremospor el termino conductivo en x.

yx

Tk

x

Tkdxdy

x

Tk

x ww

ee

n

s

e

w

∆

∂∂−

∂∂=

∂∂

∂∂

∫ ∫

esta primera integración es exacta, la aproximación se refiere a ladiscretización de las derivadas mediante:

+∆−≈

∂∂

x

TT

x

T PE

e

−∆−

≈∂∂

x

TT

x

T wp

w

susti tuyendo estas expresiones se obtiene:

yx

TTk

x

TTkdxdy

x

Tk

xWP

wPE

e

n

s

e

w

∆

∆−−

∆−≈

∂∂

∂∂

−+∫ ∫

en forma simi lar se puede demostrar que el termino conductivo en ladirección y, se puede discretizar mediante:

xy

TTk

y

TTkdydx

y

Tk

ySP

sPN

n

e

w

n

s

∆

∆

−−∆

−≈

∂∂

∂∂

−+∫ ∫

Finalmente, el termino de fuente puede ser discretizado con ayudadel teorema del valor medio para una integral ,

( ) ( ) yxSTSdxdySTS cPP

n

s

e

wcp ∆∆+≈+∫ ∫

Susti tuyendo las expresiones discretizadas en la ecuación original seobtiene:

( ) 0=∆∆++∆

∆−

−∆

−+∆

∆−

−∆−

−+−+ yxSTSxy

TTk

y

TTky

x

TTk

x

TTk cPP

SPs

PNn

WPw

PEe

que en forma canónica se puede expresar mediante:

bTaTaTaTaTa wWEESSNNPP ++++=

+∆∆

=y

xka n

N

−∆∆

=y

xka s

S

+∆∆

=x

yka e

E

−∆∆

=x

yka w

W

yxSaaaaa PWESNP ∆∆−+++=yxSb c ∆∆=

La metodología de los volúmenes fini tos de control en el caso de dosdimensiones puede ser acometida con el uso de las computadoras,mediante el cálculo sistemático de los coeficientes de influencia, (a’s)y la solución del sistema e cuaciones emergentes de ladiscretización.Para el cálculo manual, cuando se trata de un número reducido devolúmenes fini tos de control , es preferible uti l izar un procedimientoal ternativo, que se fundamenta en el balance de energía en cada unode los volúmenes fini tos de control que se emplea en ladiscretización. Este procedimiento al ternativo es i lustrado mediante elsiguiente ejemplo.

Ejemplo. La sección mostrada en la f igura es un componente básicodel aislamiento que se encuentra alrededor de un ducto cuadrado,cuyas partes superior izquierda e inferior derecha estánperfectamente aisladas. La superficie interna es isotérmica y seencuentra a una temperatura, CTh °= 20 y la superficie externa es

isotérmica y se encuentra a una temperatura, CTc °= 0 . El diseño está

caracterizado por mKWk /5,0= y .20cmL = Empleando el método delos volúmenes fini tos de control , calcule la distribución detemperaturas y la transferencia de calor desde hT a cT .

Ducto cuadrado

cT

cT

hT

hTL

L

2

L

2

L

aislante

aislado

aislado

Datos: mKWkmLCTCT ch /5,0,20,0,0,20 ==°=°=

Solución:

A continuación se muestra la discretización empleada para laresolución del problema:

1

2 3

aq bq

cq

dq

eq

fq

gq

hqSobre la discretización; aprovecharemos la simetría térmica quepresenta el problema, la cual determina que 31 TT = .

Balance de energía sobre el Volumen de control 1

1aq bq

cq

El balance de energía sobre el volumel de control 1, establece:

0=−− cba qqq

donde :

4

)( 1

LTT

kAq caa

−≈

4

)( 1

LTT

kAq hbb

−≈

2

)( 21

LTT

kAq cc

−≈

que al real izar la susti tución por los valores numéricos determina:

01,005,0

20

05,0

0 2111 =

−−−−− TTTT

kA

Balance de energía sobre el Volumen de control 2

2

cq

dq

eq

fq

El balance de energía sobre el volumel de control 2, establece:

0=−−+ efdc qqqq

donde :

4

)( 2

LTT

kAq cdd

−≈

4

)( 12

LTT

kAq ff

−≈

4

)( 2

LTT

kAq cee

−≈

que al real izar la susti tución por los valores numéricos determina:

01,005,0

0

1,005,0

0 122212 =

−−−+−+− TTTTTT

kA

Resolviendo el sistemas de dos ecuaciones con dos incognitas, seobtiene:

CT °= 5714,81

CT °= 8571,22

El calor transferido entre cT y hT , se puede determinar mediante unbalance de calor global , el cual establece :

( )hedahc qqqqq +−+=− 4

o también, por:

( ) bgbhc qqqq 8=+=−

Es indudable que la úl tima expresión, es más senci l la de evaluar, enconsecuencia;

mWL

TTkAqq h

bbhc /42,91

4

20,0205714,8

10,05,08

4

)(88 1 =−⋅⋅⋅=−==−

Factor de forma para conducción bidimensional

En la l i teratura es frecuente encontrar soluciones analíticas asoluciones de interés práctico en ingeniería. En particular, el factorde forma permite calcular el calor transferido entre la superficie quese encuentra a 1T y la superficie que se encuentra a 2T , mediante:

)( 21 TTkSq −=

donde S corresponde al factor de forma y el cual viene expresado enunidades de longi tud.

También es posible identi ficar una resistencia térmica para el caso en2-D, mediante:

SKR D

12 =−

A continuación se presenta un selecto grupo de Factores de forma:

Caso 1Placa plana

L

W

1T

2T

H

A

Restricciones: 5≥L

H, 5≥

L

W Factor de forma :

L

AS =

Caso 2Cilindro isotérmico horizontalEnterrado en un medio seminfini to

2T

z

L

D

1T

Restricciones DL >> Factor de forma: )/(cosh/2 1 DzLS −= π

Caso 3Cilindro vertical en un medio semiinfini to

2T

L 1T

DRestricciones DL >>

Factor de forma: )/4ln(/2 DLLS π=

Caso 4Conducción entre dos cil indros de longitud L en un medio infini to

1T

2T

1D 2D

WRestricciones: bDDL 21 ,>> , WL >> Factor de forma :

−−=

−

21

22

21

21

2

4cosh

2

DD

DDW

LS

π

Caso 5Cilindro circular horizontal de longi tud L, en medio de planosparaleleos de igual longi tud y ancho infini to

1T

1D

2T

2T

∞∞

∞∞

z

z

Restricciones: 2/Dz >> , zL >> Factor de forma :

=

D

z

LS

π

π8

ln

2

Caso 6Cilindro circular horizontal de longi tud L, centrado en un sólidocuadrado paraleleos de igual longi tud.

1T

1D

2T

W

Restricciones: DW > , WL >> Factor de forma :

⋅

=

D

W

LS

08,1ln

2π

Caso 7Cilindro circular excéntrico

D

d

1T 2T

z

Restricciones: dD > , DL >> Factor de forma :

−+=

−

dD

zdD

LS

2

4cosh

2222

1

π

Caso 8Conducción a través de la esquina de paredes contiguas

D

L

L

1T

2T

Restricciones 5/LD > Factor de forma ; DS 54,0=

Caso 9Conducción entre la esquina de tres paredes con di ferencia detemperaturas a traves de las paredes

L

L

L

Restricciones: ensionesotrasL dim<< Factor de forma LS 15,0=

Caso 10

Disco de diámetro D y 1T sobre un medio seminfini to de

conductividad térmica k y 2T .

Restricción: ninguna Factor de forma: DS 2=

Caso 11Esfera enterrada en un medio seminfini to

z

2T

1T

D

Ejemplo:

Con relación al problema anterior. Se pide calcular el calortransferido empleando los factores de forma tabulados en la Tabla 4.1del l ibro de Incropera. Comente sus resul tados.

Solución:

)2(4 paredesq SSTkq +∆=

m

WTkq 6,101)254.0(4 =+∆=

k

2T

∞

∞ ∞

D

El resul tado obtenido por vía numérica correspondió a 91,4 W/m, demanera que posee un error del 10% comparado con el cálculorealizado por factor de forma.

Conducción Transitoria

Muchos de los problemas más prácticos de conducción de calor noimpl ican el flujo de calor estacionario entre dos receptáculos térmicossino en vez de eso la repuesta transi toria a los cambios detemperatura. La calefacción de los edi f icios, el proceso de cocción delos alimentos, el vaciado de hierro de fundición y el tratamientotérmico de los metales (recocido, temple, revenido, etc.), todos ellosson casos en donde la tasa se cambio de la temperatura con elt iempo son importantes.En esta sección presentaremos un anál isis denominado formulaciónconcentrada que consti tuye un análisis simpl i f icado al problema deconducción transi toria.

Formulación Concentrada. Resistencia interna despreciable.

En la f igura 2.20 se muestra un cuerpo de forma arbi traria queinicialmente se encuentra a una temperatura inicial iT y que essumergido en un recipiente de grandes dimensiones que se encuentraa una temperatura ∞T . Se satisface que ∞> TTi de manera que elcuerpo estará sometido a un proceso de enfriamiento.

∞T h

)(tTT =

)0(TTi =

Análisis de Resistencia interna despreciable

La hipótesis más importante que se real iza en el análisis deResistencia interna despreciable, es que se considera que ladistribución de temperatura dentro del cuerpo es uni forme, de talmanera que la temperatura depende exclusivamente del t iempo, estasuposición en principio es aceptable bajo las siguientes condiciones:

• Cuerpo de dimensiones pequeñas• Al ta conductividad térmica del cuerpo• Bajo coeficiente de transferencia de calor por convección.

El balance de la primera Ley de la Termodinámica establece:

dt

dUqsale =−

)( ∞−= TThAq ssale

dt

dTVC

dt

dU ρ =

De tal manera que susti tuyendo, se t iene:

)( ∞−−= TThAdt

dTVC sρ

)( ∞−−= TTVC

hA

dt

dT s

ρ

La ecuación anterior permite determinar la distribución detemperaturas, como la ecuación di ferencial anterior es de primerorden se necesi ta imponer de una condición inicial , esta es:

0, == tTT i

incorporando las siguientes variables adimensionales

∞

∞∗

−−=

TT

TT

i

θ

As

VLc

k

hLcBim == ;

2Lc

tFom

⋅= α

La longi tud característica corresponde a la relación Volumen/ áreasuperficial , del cuerpo y mBi y mFo corresponden al Número de Biotmodif icado y al Número de Fourier modif icado respectivamente.

La ecuación y su correspondiente condición inicial se transformaahora en:

∗∗

−= θθm

m

BidFo

d

1)0( =∗θ

Cuya solución viene dada por:

)exp( mmFoBi−=∗θ

Interpretación Física del Número de Biot y del Número de Fourier.

mBi se denomina el Número de Biot, modificado el cual posee lasiguiente interpretación física.

]convecciónpor ia[Resistenc

]conducciónpor aResistenci[=mBi

h

k

Lc

Bim 1=

De manera que, si

1>>mBi Impl ica que: resistencia por conducción domina.

1<<mBi Impl ica que: resistencia por conducción es despreciable.El Número de Fourier modif icado es un t iempo adimensional.

En donde α , es la di fusividad térmica del material , la cual es unapropiedad térmica del sólido, que se define como:

C

k

ρα ==

almacena] que energia La

conduce] que energia La[

Determinación del calor total

Con frecuencia interesa calcular el flujo de calor total , el cual sedefine como:

∫=t

o

qdtQ

El calor anterior se puede determinar mediante un balance de primeraley entre el tiempo inicial y el t iempo final ,el cual establece que:

)( TTmCQ i −=

que expresado en variable adimensionales, puede ser escri to como:

) Bi- exp( 1 m mFoQ

Q −=∞

donde

)( ∞∞ −= TTimcQ

Expresa el número de calor que puede ser transferido por el cuerpo,que se presenta cuando transcurre un tiempo lo suficientementelargo, ∞→ t , en donde se alcanza el equi librio térmico y por tanto elcuerpo adquiere la temperatura del medio circundante.

En general se acepta que la teoría de la resistencia internadespreciable es válida siempre y cuando el número del mBi sea inferiora 0.1Cri terio para la aplicación del análisis de resistencia internadespreciable:

1.0<mBi

Cálculo de la Longitud característica para las geometrías primarias, Lc.

Placa plana.

A

L2

Longitud característ ica para una pared plana de ancho 2L

Para este caso el Volumen del cuerpo viene dado por )2( LAV =Y el área superficial por, AAs 2= , de manera que la longitud característica para lapared plana es L, es decir el semiespesor.

A continuación se resume las longitudes características para las restantesgeometrías primarias.

Geometría Volumen Area Superficial Lcplaca infinita LA2 A2 L

cilindro infinito LR2π RLπ2

2

R

esfera 3

3

4Rπ

24 Rπ3

R

Ejemplo. Unas esferas de acero al cromo( 50=k W/mk , 5103.1 −⋅=αsm /2 ) van a ser sometidas a un tratamiento térmico. Ellas son calentadas hasta

una temperatura de 650 OC y entonces son templadas en un baño de aceite quetiene una temperatura de 55 OC. Las esferas tienen un diámetro de 4.0 cm. Elcoeficiente de transferencia de calor por convección entre las esferas y el baño es,h= 300 kw/m2 . Se pide determinar (a) El tiempo que las esferas debenpermanecer en el baño para que su temperatura alcance los 200 oC, (b) El calortotal removido de cada esfera durante este intervalo de tiempo, y (c) El flujo de

calor instantáneo desde las esferas cuando ellas son colocadas en el baño ycuando alcanzan los 200 C.

Solución

Primero debe verificarse, si el análisis de resistencia interna despreciable, aplicapara este caso:

04.0 50

)3/02.0( 300

)3/( ===

k

RhBim

Dado que el número de Biot modificado es inferior a 0.1. Las ecuacionesdeducidas en esta sección pueden ser empleadas.

El número de Fourier viene dado por:

ttR

t

L

tFo

cm ⋅=⋅=⋅=⋅=

−

293,0)3/02.0(

103.1

)3/(

5

22

αα

el tiempo requerido para alcanzar las esferas una temperatura de 200C es dadopor la ecuación:(a)

)293,004,0exp()exp(55650

55200tFoBi mm ⋅⋅−=−=

−−=∗θ

Así que despejando de la ecuación anterior, el tiempo t, se obtiene, t=120,5 s, quecorresponde a un número de Fourier modificado de, 31,35=mFo

(b) La cantidad de calor total transferido al cabo de 120,5 s

)( )( )( ∞∞∞ −=−=−= TTVk

TTVcTTcmQ iii αρ

sWQ ⋅⋅=−⋅

= −43

51066,7)55650)()02,0(

3

4(

103,1

50 π

y

756,0)31,3504.0exp(1)exp(1 =⋅−−=−−=∞

mmFoBiQ

Q

así que

sWQ ⋅⋅=⋅⋅= 1079,51066,7756,0 44

(c) el flujo de calor instantáneo para t=0, mFo , es

WTThAsq i 897)55650()02,0(4300)( 2 =−⋅=−= ∞ π

y para t=120,5 s ( )31,35=mFo

WTThAsq 218)55200()02,0(4300)( 2 =−⋅=−= ∞ π

Conducción no estacionaria 1-D: Análisis distribuido

Placa plana

t

T

x

T

∂∂=

∂∂

α1

2

2

LxTThx

T

xx

T

tTT i

=−=∂∂−

==∂∂

==

∞ ,)(

0,0

0,

Introduciendo el siguiente conjunto de variables adimensionales:

∞

∞

−−

=TT

TT

i

*θ , L

xx =*

2,

L

tFo

k

hLBi

α==

La ecuación de la energía adquiere la forma:

0

*

2

*2 1

Fx ∂∂=

∂∂ θ

αθ

1,

0,0

0,1

***

*

**

*

=−=∂∂

==∂∂

==

xBix

xx

Foi

θθ

θ

θ

La solución viene expresada de la siguiente manera

)exp()cos( 2*

1

* FoxC nnn

n ξξθ −= ∑∞

=

donde nξ corresponden a los autovalores del problema, los cuales vienen dadospor: la solución de la siguiente ecuación trascendental:

( ) Binn =ξξ tan

La evaluación de la solución analítica es laboriosa porque requiere en primer lugarla determinación de los autovalores para después proceder a la evaluación de loscoeficientes nC ,Los cuales se determinan mediante,

)cos()(

)(2

nnn

nn

sen

senC

ξξξξ

+=

Para tiempos prolongados , la solución en serie converge muy rapidamente. Demanera que con la evaluación de el primer término de la serie se logra buenaexactitud.

Diagramas de Heisler

Precisamente, Heisler se dio a la tarea de graficar dichas soluciones con laevaluación del primer término, este análisis es válido para 2.0≥Fo , el cualdetermina:

)exp()cos( 21

*11 FoxC ξξθ −≈

la temperatura en el centro de la placa,

)exp( 211

*0 FoC ξθ −=

Diagramas de Heissler para la solución de problemas deconducción transitoria.

Cuando el número de Biot modificado, descrito en la sección anterior supera elvalor de 0,1, la resistencia interna ya no es despreciable, de manera que hay querecurrir a los diagramas de Heisler .

Las tres geometrías que tienen mayor importancia práctica son:

1. Una placa infinita de espesor 2L para la cual T=T(x,t), donde x es medidodesde el centro de la placa.

2. Un cilindro infinito de radio, or , para el cual T=T(r,t)

3. Una esfera sólida de radio, or , para la cual T=T(r,t)

Para la aplicación de los diagramas de Heisler deben determinarse los númerosde Biot y los números de Fourier .

Para cuyo caso las longitudes características para el empleo de los diagramasvienen dada por:

Geometría Lc

Placa infinita LCilindro infinito orEsfera or

Cálculo del calor total

El cálculo del calor total se puede realizar con la ayuda del concepto de latemperatura media.

La temperatura media, se refiere al promedio volumétrico de la temperatura, esdecir:

∫=V

m TdVV

T1

La temperatura media depende exclusivamente del tiempo, y en términos fisicoscorresponde a la temperatura que adquiriría el cuerpo si repentinamente se aislaráy se permitiera que alcanzara el equilibrio termodinámico.

En base a la temperatura media es sencillo determinar el calor total transferidopor el cuerpo, el cual mediante un balance global puede ser determinado por.

)( mi TTcmQ −=

que en terminos adimensionales puede ser reescrito mediante:

*1)(

)(m

i

m

TTcm

TTicm

Q

Q θ−=−−

=∞∞

Ejemplo. Un cilindro de hierro de gran longitud y diámetro 20 cm. Se encuentrainicialmente a 400 oC. La superficie exterior del cilindro es enfriada por aire que seencuentra a una temperatura de 50 oC y determina un coeficiente de transferenciade calor por convección de, h= 420 KmW 2/ .Si el aire es mantenido sobre el cilindro por espacio de 20 min. Determine (a) Latemperatura en el eje del cilindro y en su superficie, y (b) La cantidad de calor totalpor unidad de longitud transferido por el cilindro durante los 20 min. que duro elproceso.

Datos

K= 70 KmW /

s/m 102 25−⋅=αkmc 25 /J 1035 ⋅=ρ

D= 0.20 m

CT 50=∞

KmWh 2/ 420=

C 400=iT

Solución

s 12006020 =⋅=tmro 10,0=

En primer lugar vamos a calcular el mBi .

1.030,070

)2/10,0(420)2/( >>===k

rohBim

por tanto el análisis de resistencia interna despreciable no puede ser empleado yhay que recurrir a los diagramas de Heisler .

Para ello debemos calcular los Números de Biot y de Fourier , empleando el radio,ro como longitud característica.

(a)

60,070

10,0420 =⋅=⋅=

k

rohBi

40,210,0

1200102

2

5

2=⋅⋅=⋅=

−

ro

tFo

α

Vamos a los diagramas de Heisler correspondientes a un cilindro.

En la figura D.4 entramos con 40,2=Fo y 667,11 =Bi

y leemos la temperatura

adimensional del eje del cilindro ),( torTTo ==

Obteniéndose:

11,00 =−−

∞

∞

TT

TT

i

despejando, 0T

CT 5,885011,0 )50400(0 =+−= Conocido el valor de 0T , nos queda por determinar

la temperatura en la superficie, Ts , ),( torTTs ==

Este procedimiento se realiza empleando la Figura D5.

Para este caso se entra a la gráfica con el inverso de Biot , 667,11 =Bi

, y

especificada la curva 1/ =ror , se lee

75,00

=−−

∞

∞

TT

TT

Se calcula CtrorTT °=+−=== 7950)505,88( 75,0),1/(

(b) Para el cálculo del calor total, se emplea la Figura D6, en dicha gráfica se entracon FoBi2 (abcisa) y se especifica la curva correspondiente al Bi , para estecaso, se tiene:

8640,040,2)06,0( 22 =⋅=FoBi

60,0=Bi

Leyéndose

9,0=∞Q

Q

y

m

sWTTroC

L

Qi

⋅⋅=−⋅= ∞∞ 72 1085,3)(πρ

por lo tanto,

m

J

L

Q 77 1046,31084,39,0 ⋅=⋅⋅=

Aunque no lo pedía el problema es ilustrativo determinar la temperatura media.

1,09,011Ti

=−=−=−−

∞∞

∞

Q

Q

T

TTm

Por tanto, CTm °= 85 .

Conducción transitoria en dos y tres dimensiones

Hasta aquí hemos discutido tan solo el flujo de calor unidimensional en paredes,

cilindros y esferas. No obstante muchos problemas prácticos se incluyen flujo de

calor en dos y tres dimensiones. Bajo ciertas condiciones especiales, la solución

de problemas de conducción transitoria en dos y tres dimensiones, puede ser

obtenida por la superposición del producto de soluciones de problemas

unidimensionales.

Vamos a ilustrar con un ejemplo, considere el cilindro finito mostrado en la Figura.

La solución para el cilindro finito puede ser obtenida como el producto de la

solución para una placa infinita y la solución de un cilindro infinito.

Figura Cil indro f inito formado por la intersección de un ci l indroinfinito con una placa infinita.

De manera que para esta situación se tiene:

initocilindroi

initaplacaii TT

TtrT

TT

TtxT

TT

TtxrT

infinf

),(

),(

),,(

∞

∞

∞

∞

∞

∞

−−⋅

−−=

−−

L2

or2

r

x

El principio de superposición descrito anteriormente puede ser aplicado a otrassituaciones, tales como las indicadas a continuación

Barra rectangular formada por el producto de dos placas infinitas.

initaplaca

initaplaca TTi

TtyT

TTi

TtxT

TTi

TtyxT

infinf

),(),(),,(

∞

∞

∞

∞

∞

∞

−−⋅

−−=

−−

Paralelepípedo formado por el producto de tres placas infinitas.

initaplaca

initaplaca

initaplaca TTi

TtzT

TTi

TtyT

TTi

TtxT

TTi

TtyxT

infinfinf

),(),(),(),,(

∞

∞

∞

∞

∞

∞

∞

∞

−−⋅

−−⋅

−−=

−−

El principio de superposición descrito en esta sección es aplicable sólo ensituaciones en las cuales la temperatura inicial sea uniforme y que todas lassuperficies estén expuestas al mismo ambiente convectivo.

El cálculo del calor total para el caso de situaciones multidimensionales se puederealizar aplicando el principio del producto de soluciones a la temperatura media.De manera que una vez determinado la temperatura media, el calor total puedeser determinado por :

)( mi TTmcQ −=

Ejemplo. Un cilindro de hierro de longitud 10 cm y diámetro 20 cm, se encuentrainicialmente a 400 oC. La superficie exterior del cilindro es enfriada por aire que seencuentra a una temperatura de 50 oC y determina un coeficiente de transferenciade calor por convección de KmWh 2/ 420= .Sí el aire es mantenido sobre el cilindro por espacio de 20 minutos. Determine latemperatura en el centro geométrico del cilindro y el calor total transferido.

Datos

kmWk / 70=sm / 102 25−⋅=α

kmJc 25 / 1035 ⋅=ρ

Solución:

La solución al problema viene dada por:

initocilindroi

initaplacaii TT

TtoT

TT

TtoT

TT

TtooT

infinf

),(

),(),,(

∞

∞

∞

∞

∞

∞

−−⋅

−−=

−−

Es importante calcular en forma independiente el Número de Fourier y el de Biotpara cada solución por separado.

Cilindro inf inito de radio ro=0,10 m:

Biot y Fourier ya fueron calculados en el ejemplo anterior

6667,1/1 60,0 == BiBi

40,2=Fo

Leyendo de la gráficas se tiene:

11,0),(

inf

=−

−

∞

∞

initocilindroi TT

TtoT

y la Temperatura media ya ha sido calculada

10,0=−−

∞

∞

TT

TT

i

m

Placa plana de espesor 0,1 m

Para este caso la longitud característica para entra en los diagramas de Heisler esel semiespesor, por tanto L=0,05 m

3,070

05,0420 =⋅=⋅=k

LhBi

6,905,0

12001022

5

2=⋅⋅=⋅=

−

L

tFo

α

y leyendo en la Figura D.1

se tiene:

07,0),(

inf

=−

−

∞

∞

initocilindroi TT

TtoT

0077,0)11,0)(07,0(),(

),(),,(

infinf

==−

−⋅

−−

=−

−

∞

∞

∞

∞

∞

∞

initocilindroi

initaplacaii TT

TtoT

TT

TtoT

TT

TtooT

por tanto T(0,0,1200s)=0,063(400-50)+50=52,7 C

La temperatura del centro es de 52,7 C

Y la temperatura media, se obtiene siguiendo un procedimiento similar,

001,0)01,0)(1,0( infinf

==−−

⋅−−

=−−

∞

∞

∞

∞

∞

∞

initocilindroi

m

initaplacai

m

i

m

TT

TT

TT

TT

TT

TT

JQ 5105,38 ⋅=

Sólido seminfinito

La solución de la distribución de temperaturas en un sól idoseminfini to, es de gran ayuda para la determinación de la temperaturaen sól idos fini tos para t iempos pequeños. En el pasado habíamoscomentado que la solución de sól idos fini tos para t iempos pequeños,( 2.0<<Fo ) requería la evaluación de muchos términos de la serie,dado que la convergencia de la serie que determina la solución sedi f icul ta en la medida que el t iempo sea más cercano a cero..

En términos físicos, cuando el t iempo es relativamente pequeño; latemperatura del cuerpo suficientemente ale jada de la paredcorresponde a la temperatura del cuerpo para el instante inicial , iT ,tal como se señala en la Figura, en la cual se observa un sól idoseminfini to sometido a una temperatura superficial constante en lapared, ST .

xiT

sT

∞La formulación matemática de este problema viene dada por:

t

T

x

T

∂∂=

∂∂

α1

2

2

∞→===

==

xTT

xTT

tTT

i

S

i

0

0

La solución de este problema , puede ser obtenida anali t icamente conla ayuda del siguiente cambio de variable;

t

x

αη =

la cual determina que la ecuación en derivadas parciales original ysus condiciones iniciales y de frontera se conviertan en :

ηη

η d

dT

d

Td

22

2

−=

0==∞==

ηη

S

i

TT

TT

que como se observa corresponde a una ecuación di ferencialordinaria, donde la variable independiente es, η .

Si se introduce la nomenclatura, ηd

dTT =' , la ecuación se puede

rescribir despues de realizar separación de variables, como:

ηηd

T

Td

2'

)'( −=

que al integrar se obtiene:

1

2

ln4

'ln cT +−= η

que al despejar y devolver el cambio de variables, se t iene

)4

exp(2

1

ηη

−= Cd

dT

e integrando una vez más,

20

2

1 )4

exp( CdCT +−= ∫ ηηη

donde 1C y 2C pueden ser determinadas de las condiciones decontornos.

La solución anterior incluida el cálculo de las constantes puede serexpresada mediante la función error, como :

)2

(t

xerf

TT

TT

Si

S

α=

−−

donde la función error, es definida mediante:

dmmxerfx

)exp(2

)(0

2∫ −=π

En la f igura se muestra la solución, en el la se observa que paravalores de

0 0.5 1 1.5 2 2.5 30

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

x/2(α t)0.5

(T-T

S)/

(Ti-T

S)

22

=t

x

α

La solución se hace prácticamente igual a la unidad, que en términosfísicos corresponde a que la temperatura se asemeja a la temperaturainicial , iT . Con esta observación se puede desarrol lar un cri terio paradecidir cuando un sólido puede ser considerado como seminfinto, elcual se puede expresar mediante la siguiente desigualdad:

22

>t

L

α

Alternativamente, introduciendo la definición del número de Fourier,2/ LtFo α= , es posible reescribir el cri terio como:

16

1<Fo

Que puede interpretarse como que la solución para tiempos pequeñosse puede obtener mediante la correspondiente a un sólidoseminfini to; si se cumple que el número de Fourier es inferior a 1/16.

La determinación del calor, en la pared del sól ido puede serdeterminado mediante la ley de Fourier:

t

TTk

x

Tkq iS

xS πα

)(

0

" −=

∂∂−=

=

Los casos de flujo de calor constante en la pared y ambienteconvectivo pueden ser encontrados en la pag 239 del l ibro deIncropera.

Ejemplo. Una compañia de seguros lo contrata a Ud. como asesorpara entender y saber más sobre las lesiones por quemaduras. Estáninteresados en especial por las lesiones inducidas cuando una partedel cuerpo de un trabajador l lega a hacer contacto con maquinariaque está a temperaturas elevadas en el rango de C°50 a C°100 . Elasesor médico les informa que ocurri rá una lesión térmicairreversible en cualquier tejido vivo que se mantenga a CT °≥ 48

durante 10 s. Quieren informacón con respecto al grado de dañoireversible del tejido(medido por la distancia desde la superficie de lapiel) como función de l a temperatura de la maquinaria y el t iempoduramte el cual se t iene contacto entre la piel y la maquinaria.Suponga que el tejido vivo t iene una temperatura normal de 37 C° , esisotrópico y t iene propiedades consantes equivalentes al agualíquida. (a) para evaluar la seriedad del problema, calcule lugares enel tejido en los que la temperatura alcanzará C°48 .Solución.

De la tabla A.6 KCT 31037 ≈°=3/1,993

1mkg

vf

==ρ , kgKJc /4178= , mKWk /628,0=

smc

k/10513.1 27−⋅==

ρα

Caso #1

)2

(t

xerf

TT

TT

Si

S

α=

−−

para CTS °= 100 , solución gráfica (fig 5.8) ∞→ TTS , por tanto ∞→h

con este valor se obtiene de la gráfica que 0.1)2

( =t

xerf

α, lo que

determina que:

mmx 46,2=

Solución anal i tica:

825,0=−−

Si

S

TT

TT

en la Tabla B.2 (B.3) erf(x)=0.825 96.0=⇒ w .36,2 mmx =

de forma simi lar para CTs °= 50 se obtiene por la vía analítica:

1746,0=−−

∞ i

i

TT

TT

mmx 34,0=Discretización para conducción transitoria

Caso 1-D estacionario

0)(1 =++ cp

nn

STSdr

dTkr

dr

d

r

Ecuación discretizada

bTaTaTa WWEEPP ++=

1-D transi torio

t

TcSTS

dr

dTkr

dr

d

rcp

nn ∂

∂=++ ρ)(1

La discretización del termino transi torio se realiza mediante elmétodo impl ici to (método de Euler); el cual consiste en la derivadaatrasada de la temperatura con respecto al t iempo.

t

TT

t

T

∆−≈

∂∂ 0

que al susti tuir en la ecuación 1-D transi torio se tiene:

t

TTcSTS

dr

dTkr

dr

d

rcp

nn ∆

−=++0

)(1 ρ

Esta se puede reescribir como:

0)(1 ** =++ cp

nn

STSdr

dTkr

dr

d

r

donde ahora;

t

cSS PP ∆

−= ρ*

0* Tt

cSS cc ∆

+= ρ

Es decir con estas pequeñas modificaciones se puede incorporar eltermino transi torio en un programa que resuelva problemasestacionarios.

Es importante destacar que cuando ∞→∆t , la formulación coincidecon la correspondiente a condiciones estacionarias.

Procedimiento

1. Dado 0T (condición inicial) y t∆ se calculan *PS y *

CS2. Se determinan los coeficientes de influencia (a’s) y se resuelve el

sistema de ecuaciones, para obtener así un nuevo campo detemperaturas

3. El nuevo campo de temperaturas pasará a ser 0T y se regresa a1. Y se prosigue hasta alcanzar el tiempo deseado.

La aplicación de este procedimiento es idéntica para el caso de 2-D y3-D.

Convección

Definición de convección : Mecanismo de trasferencia de calor quese caracteriza por la presencia de una pared a una temperatura daday de un fluido en movimiento que incide sobre dicha pared.

sT

cq

∞U ∞T

∞> TTs

Definición de convección

∞T : Denota a la temperatura de la corriente no perturbada

∞U : Denota la velocidad de la corriente

Las condiciones de corriente l ibre se suceden en los valores de ∞U y

∞T no cambian.

La ecuación de Newton establece:

)( ∞−= TThAsq s

Es importante recordar el carácter empírico que tiene la ecuación deNewton

Clasificación de la convección.

A continuación se presenta un diagrama que esquematiza laclasi ficación de la convección:

Convección

Forzada

Naturalo

Libre

Interna

Externa

Interna

Externa

Clasificación de la convección

Se denomina convección forzada a la convección en donde el fluidoes inducido por un agente mecánico. Ej. Bomba, Venti lador.

Se denomina convección natural o l ibre aquella donde el f lujo seinduce por cambio de densidades.

El adjetivo interno y externo se refiere al confinamiento del flujo. Si lacirculación del f luido se realiza a través de un espacio cerrado Ej.Tubería, se dice que el f lujo es interno, por el contrario si el f lujo nose encuentra confinado, se le da el adjetivo de externo. Ej. El f lujo deaire impulsado por un venti lador.

A continuación se presentan los valores típicos del coeficiente detransferencia de calor por convección, h

Valores Típicos de h

Proceso )/( 2kmWh

Convección naturalGases 2-25Líquidos 50-1000

Convección ForzadaGases 25-250Líquidos 50-20000

Convección con cambios de faseEbul lición o Condensación 2500-100000

Número de Nusselt.

El número de Nusselt corresponde al coeficiente de transferencia decalor por convección adimensional y se determina de la siguientemanera.

y

convcond qq =

Figura 4.2 Número de Nusselt

Real izando una equivalencia entre el calor que se transmite porconducción y el determinado por convección se tiene:

pared )(y

TAkTThA fs ∂

∂−=− ∞

Es importante destacar que la ecuación anterior no proviene de unbalance de calor, sino de una equivalencia entre el mecanismo deconducción en la pared y la ecuación empírica de Newton.

De la ecuación anterior se desprende que:

∞−∂∂−

=TT

y

Tk

hs

paredf

Antes de seguir adelante es conveniente reconocer que según laecuación anterior el coeficiente de transferencia de calor porconvección, h depende de la conductividad térmica del f luido de ladi ferencia de temperaturas y del gradiente de temperaturas en lapared. Precisamente, esta úl t ima dependencia nos hacer intuir ladependencia indirecta con la distribución de velocidades ya que laforma que adquiera la distribución de temperatura dependerá del

perfi l de velocidades en las inmediaciones de la pared. Es estaobservación la que permite reconocer la intima relación entre elproblema Fluidodinámico y el problema térmico, presentes en laconvección.

Siguiendo adelante, realizaremos una adimensional izaciónconveniente de la ecuación anterior.

Si en la ecuación anterior se introducen las siguientes variablesadimensionales;

∞

∞

−−

=TT

TT

s

θ ; Temperatura adimensional

L

yY = ; Coordenada adimensional

donde L es una longi tud característica convenientementeseleccionada.

La ecuación se transforma a:

LY

Tk

hyf 0=∂

∂−=

Reescribiendo la ecuación anterior se obtiene:

0=∂∂−==

yf Yk

hLNu

θ

Donde, Nu, designa al Número de Nusselt.

Wilhelm Nusselt , Ingeniero Alemán que real izo notablescontribuciones al estudio de la transferencia de calor, otorgándole ensu honor al parámetro adimensional, hL/kf, el nombre de número deNusselt.

En general el estudio de la convección pretende determinar h, o bienen forma adimensional, el número de Nusselt.

Métodos de obtención del Número de Nusselt . Existen dos formas de determinar el número de Nusselt, una de ellas es la experimental , la cual da lugar a correlaciones empíricas y la otra mediante el modelaje matemático que implica la resolución de las ecuaciones diferenciales que gobiernan el fenómeno fluidodinámico y el fenómeno térmico. La integración de dichas ecuaciones se realiza mediante técnicas numéricas. El método experimental, consiste en realizar experiencias que involucran al proceso de convección que se desee estudiar, generalmente se realiza previamente un análisis dimensional, con la ayuda del Teorema de π -Buckingham para así, determinar la dependencia del Número de Nusselt con los demás parámetros adimensionales que caracterizan el problema estudiado. Este proceso es costoso, pero a la vez es sencillo porque no requiere conocer a fondo las ecuaciones que rigen el proceso. En cambio la técnica de simulación numérica es relativamente económica, ya que cambiar una condición del proceso, por decir una temperatura, implica solamente teclear un dato en la computadora. Ahora obviamente, el resultado será confiable en la medida que el modelo matemático reproduzca al proceso real. Afortunadamente, hoy en día, con el desarrollo espectacular que ha tenido la computación, es posible realizar simulaciones que antiguamente eran imposibles de pensar. Dada la complejidad del tema, en este capitulo nos limitaremos a presentar las correlaciones más populares y para las situaciones más corrientes. El lector interesado puede ampliar los conocimientos consultando los libros recomendados en la bibliografía. También es cierto que constantemente se realizan nuevas contribuciones, que se publican periódicamente en las diferentes revistas especializadas en el área de transferencia de calor. Correlaciones de Convección Forzada El propósito de esta sección es presentar una colección de las relaciones más ampliamente usadas para la determinación del Número de Nusselt por convección forzada. Algunas de estas relaciones tienen bases teóricas, y otras son completamente experimentales. En ciertas circunstancias más de una ecuación será presentada, en donde se señalará la más recomendable. Las correlaciones para convección Forzada presentan la siguiente relación funcional:

Pr)(Re,fNu =

Donde: Nu : Número de Nusselt Re: Número de Reynolds, vUL / Pr : Número de Prandtl, α/Pr v= El número de Reynolds ya es familiar para nosotros, así que dedicaremos las próximas líneas a comentar el significado del numero de Prandtl, Pr Interpretación del número de Prandtl . El número de Prandtl, es un número adimensional que involucra a la viscosidad cinemática del fluido, con su difusividad térmica:

k

C

C

kv p

p

µ

ρ

ρµ

α====

Térmica] ad[Difusivid

] Movimiento de Cantidad de dDifusivida [Pr

A continuación se presentan valores característicos del número de Prandtl para diversos fluidos

Fluido Pr Metales líquidos Sodio 0,011 Mercurio 0,0196 Bismuto 0,0142 Gases Aire 0,70 Dióxido de carbono ( 2CO ) 0,75 Monoxido de carbono(CO ) 0,73

Helio 0,68 Hidrogeno 0,70 Agua 4,6 Fluidos viscosos Aceite de motor 3400 Glicerina 3060

En ella se puede apreciar que los metales líquidos poseen número de Prandtl muy bajos, los gases presentan la particularidad de tener un Número de Prandtl, en el entorno de 0,7, el agua, valores intermedios y finalmente los valores mayores del número de Prandtl lo presentan los fluidos viscosos. Convección forzada externa sobre una placa plana.

Flujo laminar Para esta situación se puede observar soluciones analíticas para el Nusselt local y Nusselt promedio, las cuales se han verificado experimentalmente.

3/12/1 PrRe 332,0 xxNu =

3/12/1 PrRe664,0 LLNu =

≈<

≤≤5

, 10.5ReRe

50Pr6,0

cx

donde:

k

LhNu

k

xhNu Lx

.,

. ==

v

LU

v

xULx

∞∞ == Re,Re

Las propiedades son evaluadas a la temperatura de película, 2∞+

=TT

T sf

La condición de flujo laminar se especifica claramente, en términos del número de Reynolds, 5105Re ⋅< El limite inferior de 0,6 es establecido para números de Prandtl dado que este es el menor valor que pueden tomar los gases. Para esta circunstancia se emplea.

2/12/1 PrRe 565,0 xxNu =

2/12/1 PrRe 130,1 LLNu =

≈<

≤5

, 10.5ReRe

050.0 Pr

cx

Las propiedades se evalúan igualmente a Tf Churchill y Ozoe (1973) desarrollaron una ecuación empírica que abarca todo el espectro de números de Prandtl:

100

]Pr)/ 0468,0(1[

PrRe 3387,04/13/2

3/12/1

≥+

=

x

xx

Pe

Nu

4/13/2

3/12/1

]Pr)/ 0468,0(1[

PrRe 6774,02

+== L

xx NuuN

] 100PrRe [ > Propiedades evaluadas a Tf. Flujo Turbulento. Nusselt Local Para flujo turbulento, sólo correlaciones para Nusselt local, dado que los valores promedios deben tomar en cuenta la sección laminar inicial:

753/18,0 10Re105 ,PrRe 0296,0 <<⋅= xxxNu

[ ]60Pr6,0 ≤< Capa limite mixta, laminar –turbulenta. Nusselt promedio Para una placa plana de Longitud L en la cual LRe excede del valor critico, la transferencia de calor promedio debe contabilizar la sección laminar inicial.

+= ∫∫ dxhdxh

Lh

c

c

c L

x

turb

x

lamL 1

0

Realizando la operación indicada se obtiene:

753/18,0 10Re105 ,Pr]872Re037,0[ <<⋅−= LLLNu

⋅>

≤<5

, 105Re

60Pr6,0

cx

Ejemplo 3.1 Aire a presión atmosférica a 40C fluye a una velocidad de 40 m/s sobre una placa plana de 0,75 m de largo por 0,5 m de ancho. La superficie es mantenida a 260 C° (a) Determinar el calor total transferido sobre un lado de la placa. Solución La temperatura de la película, Tf =(40+260)/2=150C A esta temperatura las propiedades del aire son:

69.0Pr,/ 1058,28, / 1059,34,/ 8342,0 2633 ==⋅== −− smxvKmWkmKgρ (a) El número de Reynolds es:

66

1005,110 58,28

75.0 40Re x

x

xL == −

dado que 5105Re xL > se debe utilizar la ecuación:

1374Pr ]872Re 037,0 [ 3/18,0 =−= LLNu

CmWxL

kNuh L

2/ 4,6375,0

03459,0 1374 ===

El flujo de calor total, es:

WTThAq s 5230)40260( )5,075,0( 4,63)( =−⋅⋅⋅=−= ∞ Correlaciones para cilindros y esferas Ver pág 366-374 del libro de texto.

Problema Una barra conductora de cobre de sección circulra de diámetro D=15 mm. Se enfria por la acción de un flujo

de aire seco. La velocidad y la temperatura del flujo incidente de aire son V= 1m/s y CT °=∞ 25 . Se pide calcular (a) el coeficiente de transferencia de calor promedio, (b) La intensidad de corriente admisible de manera que la temperatura superficial no sobrepase los C°80 . La resistividad elécctrica del cobre

corresponde a : melect ⋅Ω⋅= −81075,1ρ .

Solución:

Propiedades del aire a CTf °=+

= 522

8025

sm /1041,18 26−⋅=ν

mKWk /1015,28 3−⋅=

703,0Pr =

8,814Re =⋅=ν

DVD

Empleando la correlación de Churchill-Berstein

5/48/53/2

4/1

3/2

3/12/1

282000

Re1

Pr

4,01

PrRe62,03,0

+

+

+=DNu

39,14=DNu

202,27

m

Wh =

Estableciendo un balance entre la potencia disipada por el cable la cual debe disiparse por convección:

smV /1=

D

CTs °= 80

CT °=∞ 80

A

LITTLDh elecS ⋅⋅=−⋅⋅⋅ ∞ ρπ 2)(

De donde sustituyendo, y despejando I , se tiene AI 848= . Problema La pelotas de béisbol empleadas en las ligas mayores poseen un diámetro promedio de cm4,7 y una masa

de gr145 . La distancia entre el montículo donde se encuentra el pitcher y el cajón de bateo es de m5,18 . El pitcher frota la bola con sus manos, de suerte tal que la pelota adquiere una temperatura en su superficie de

C°30 , mientras que la temperatura del aire circundante corresponde a C°20 . El pitcher lanza una bola rápida a 80 millas/h. Suponiendo que la rotación de la bola y su movimiento vertical son despreciables,

(a) calcular la fuerza de arrastre experimentada por la pelota (b) estimar la velocidad horizontal de la pelota cuando alcanza el mascotín del catcher. (c) Suponiendo que la temperatura de la superficie no cambia, calcule el calor transferido desde la pelota

al ambiente durante el lanzamiento. Solución Propiedades del aire a C°20 ( K293 )

3/1614,1 mKg=ρ

KkgkJcp /007,1=

sPa⋅⋅= −3106,184µ

mKWk /103,26 3−⋅=

707,0Pr =

sPas ⋅⋅= −710189µ @ 303 K

smhmillasV /5,35/80 ==

cálculo del número de Reynolds

51065,1Re ⋅==µ

ρVDD

(a) de la figura 7.8 4,0=DC

NACVF fDD 26,1)074,0(4/4,0)5,35(1614,15.02

1 222 =⋅⋅⋅⋅⋅=⋅⋅= πρ

(b) De la ecuación de conservación de energia Mecánica

LFWmVmV Dof ⋅−==− 22

2

1

2

1

939222 =⋅−=

m

LFVV D

of ⇒ smVf /64,30=

(c) 4/14,03/22/1 )(Pr)Re06,0Re4,0(2S

DDDNuµµ⋅+⋅+= =293

KmWh 2/104=

WTTAhq SS 9,17)2030()0074,0(104)( 2 =−⋅⋅=−⋅= ∞ π

sF

VVmt

D

fo 56,0)(

=−

=

Jtqqt 10=⋅=

FLUJO EN BANCO DE TUBOS

La transferencia de calor en este tipo de arreglo es muy utilizada en laindustria, de hecho es uno de los tantos tipos de intercambiadores de calor.Comúnmente, un fluido fluye dentro de los tubos, mientras un segundo fluido, adiferente temperatura fluye a través de ellos. Dada externo, se especificarán lascorrelaciones, el balance de calor y la caída de presión para el flujo que fluye através de los tubos.

Para empezar se debe aclarar los dos tipos disposición, o arreglosgeométricos que pueden tener los tubos: disposición alineada y disposicióntriangular o desplazada.

FlujoExterno Flujo Interno

Banco de Tubos

U ,T

SL

ST

D

ST

SL

SD

U ,T

Disposición Alineada DisposiciónTriangular

Nomenclatura empleada en banco de tubos:

SL…Distancia entre dos hileras consecutivas.

ST…Paso transversal; distancia, transversal al flujo, entre dos cilindrosconsecutivos.

SD…Paso diagonal (sólo para disposición triangular).

NL…Número de tubos en dirección longitudinal.

NT…Número de tubos en dirección transversal.

Para los efectos de transferencia de calor la disposición triangular es máseficiente que la disposición alineada, pero la caída de presión en la primeradisposición es mucho mayor. A la hora de diseñar un banco de tubos se busca uncompromiso, una transferencia de calor eficiente, y una caída de presión baja; delo contrario se necesitará de una bomba más eficiente para transportar el flujo, loque puede implicar un incremento en los costos.

Todas las correlaciones que rigen al flujo externo a través de un banco detubos están basadas en el Re d max.

Donde :D…Diámetro de los tubosν...Viscosidad cinemáticaUmax … Velocidad máxima.

La velocidad máxima en la distribución alineada ocurre entre doscilindros, y por continuidad se tiene:

De donde, al despejar la velocidad máxima, se tiene la siguienteexpresión:

νDU

D

⋅= max

.maxRe

( )DSUSU TmaxT −⋅=⋅∞

)(max DS

SUU

T

T

−⋅

= ∞

En la disposición triangular la velocidad máxima puede ocurrir através del paso diagonal (SD) o a través del paso transversal (ST), por esose deben comparar estas distancias para calcular correctamente esteparámetro.

Por lo explicado anteriormente se debe hallar SD:

Si se cumple:

La velocidad máxima será igual que en el caso de disposiciónalineada, es decir:

De lo contrario:

U max. SL

Umax

Umax

SD

Velocidad Máxima en laDistribución Triangular

( )SS

SDT

L=

+

2

22

2

DSS T

D

−>

)(max DS

SUU

T

T

−⋅

= ∞

2

DSS T

D

−<

Y la velocidad máxima estará definida por la siguiente expresión:

Para obtener el coeficiente por convección promedio para todo el banco detubos se deben utilizar las correlaciones citadas a continuación:

• Correlación de Grimison

Restricciones:

Las propiedades se evalúan a la temperatura promedio entre la superficie y elfluido.C1 y m se obtienen de la siguiente tabla:

ST/D1,25 1,5 2,0 3,0

SL/D C1 m C1 m C1 m C1 m

Alineado1,25 0,348 0,592 0,275 0,608 0,1 0,704 0,0633 0,7521,5 0,367 0,586 0,25 0,62 0,101 0,702 0,0678 0,7442,00 0,418 0,57 0,299 0,602 0,229 0,632 0,198 0,6483,00 0,29 0,601 0,357 0,584 0,374 0,581 0,286 0,608Triangular0,600 - - - - - - 0,213 0,6360,900 - - - - 0,446 0,571 0,401 0,5811,000 - - 0,497 0,558 - - - -1,125 - - - - 0,478 0,565 0,518 0,561,250 0,518 0,556 0,505 0,554 0,519 0,556 0,522 0,5621,500 0,451 0,568 0,46 0,562 0,452 0,568 0,488 0,5682,000 0,404 0,572 0,416 0,568 0,482 0,556 0,449 0,573,000 0,31 0,592 0,356 0,58 0,44 0,562 0,428 0,574

Tabla 1

)(2 DS

SUU

D

Tmax −⋅

⋅= ∞

( )Nu CD Dmax

m= 1 Re

7.0Pr

40000Re2000

10

max

=<<

≥

D

LN

• Se ha desarrollado otra expresión, basada en la anterior, para poder utilizarlacon otros fluidos:

Restricciones:

Las propiedades se evalúan a la temperatura promedio entre la superficie y elfluido.C1 y m se obtienen de la Tabla1Si NL<10 se toma en cuenta el siguiente factor de corrección:

Donde C2 viene dado en la siguiente tabla:

NL 1 2 3 4 5 6 7 8 9

Alineado 0,64 0,8 0,87 0,9 0,92 0,94 0,96 0,98 0,99

Triangular 0,68 0,75 0,83 0,89 0,92 0,95 0,97 0,98 0,99

Factor de corrección C2 para NL<10

Tabla 2

• La correlación mas reciente es la propuesta por Zhukauskas:

Restricciones:

Todas las propiedades se evalúan a LMTD entre la entrada y la salida, exceptoPrs que es evaluado a la temperatura de la superficie.C se obtiene de la siguiente Tabla:

( )Nu CD Dmax

m= 113 1

1 3. Re Pr/

7.0Pr

40000Re2000

10

≥<<

≥

Dmax

LN

Nu C NuD D= 2

( )Nu CD Dmax

m

s

=

Re Pr

Pr

Pr.

/

0 36

1 4

6102Re1000

500Pr7.0

20

⋅<<

<<≥

Dmax

LN

Disposición ReDmax C m

Alineada 10-10^2 0,8 0,4Triangular 10-10^2 0,9 0,4Alineada 10^2-10^3 Aproximar a unTriangular 10^2-10^3 cilindro aisladoAlineada 10^3-2*10^5 0,27 0,63(ST/SL<0,7)Triangular 10^3-2*10^5 0,35(ST/SL)^1/5 0,6(ST/SL<2)Triangular 10^3-2*10^5 0,4 0,6(ST/SL>2)Alineada 2*10^5-

2*10^60,021 0,84

Triangular 2*10^5-2*10^6

0,022 0,84

Constante C para la correlación de Zhukauskas

Tabla 3

Si NL<20 se aplica el siguiente factor de corrección:

C2 se obtiene de la siguiente tabla:

NL 1 2 3 4 5 7 10 13 16

Alineado 0,7 0,8 0,86 0,9 0,92 0,95 0,97 0,98 0,99

Triangular 0,64 0,76 0,84 0,89 0,92 0,95 0,97 0,98 0,99

Factor de corrección C2 para NL<20ReD>10000

Tabla 4

Nu C NuD D= 2

Calor Transferido

Para determinar el calor transferido se realiza un balance de calor entre laentrada y la salida:

Donde:N…Número total de tubos en el bancoLMTD se determina de la siguiente manera:

Banco de Tubos

T 1 T 2

LMTDLDNhq ⋅⋅⋅⋅⋅= π

LMTDT T

T

T

T T T

T T T

Sustituyendo

LMTDT T

T T

T T

s

s

s

s

=−

= −= −

=−−−

∞

∞

∞ ∞

∞

∞

∆ ∆∆∆

∆∆

1 2

1

2

1 1

2 2

2 1

1

2

ln

:

ln

,

,

, ,

,

,

Por otro lado:

Caída de Presión:

Como se explicó anteriormente, es necesario tomar en cuenta la caída depresión que puede ocurrir durante el desplazamiento del fluido a través del bancode tubos ya que si ésta aumenta se requerirán equipos más eficientes para poderllevar a cabo el proceso, lo que puede generar mayores gastos operativos. Lacaída de presión es expresada como:

∆p N V fl max= ⋅ ⋅χ ρ( / )2 2

El factor de fricción f y el factor de corrección χ se pueden determinarcon la figura 7.13 y 7.14 para el caso de una distribución alineada y unatriangular respectivamente. Las figuras son referidas al libro “Fundamentals of heatand mass transfer” de F.P.Incropera y D.P. DeWitt, cuarta edición.

q mC T T

m U N S L

Igualando

T T

T T

hN D

U C N S

p

T T

s

s p T T

= −=

−−

= −

∞ ∞

∞

∞

∞ ∞

( )

:

exp

, ,

,

,

2 1

2

1

ρ

πρ

Convección Forzada interna en tuberías circulares.

La importancia ingenieril de la convección forzada interna en tuberías, para propósito de transporte,enfriamiento, calentamiento, es innegable. La mayoría de los ductos o tuberías utilizadas para eltransporte de gases o líquidos presentan una diferencia de temperatura con los alrededores, originándoseun flujo de calor de o hacia el fluido. En estas situaciones tanto el régimen laminar como el turbulento sesuceden.

TEMPERATURA VOLUMéTRICA MEDIA (BULK)

Se desea analizar el problema de transferencia de calor que tiene lugarcuando un fluido de trabajo circula por un conducto cerrado; tal como se ilustraa continuación:

2 R

Ts

Ts

To

A

r

x

Donde To representa la distribución de temperatura uniforme del fluido ala entrada de la tuberìa, A el área transversal de la tubería y Ts la temperaturasuperficial de la misma.

Resulta intuitivo, darse cuenta que a medida que el fluido avanza por latubería la distribución de temperaturas va cambiando; o lo que es lo mismo, elperfil de temperaturas varía con la posición. Por lo tanto, resulta necesariodefinir un parámetro que nos ayude a cuantificar (mediante un promedio) latemperatura de cada sección. Este parámetro se denomina temperaturavolumétrica media, Tb, y se define de la siguiente manera:

T b( )x

dA...ρ c U( ),r x T( ),r x

dA..ρ c U( ),r x

Conviene resaltar, que el numerador de la expresión anterior representala entalpía asociada a cada sección y el denominador la entalpía por unidad devolumen.

De tal manera, que la temperatura volumétrica media Tb representauna temperatura uniforme que caracteriza energéticamente a una sección deuna tubería. Esto significa, que el perfil de temperatura no uniforme de unasección de la tubería puede ser sustituido por la temperatura volumétricamedia.

Para estimar la temperatura volumétrica media existen tresprocedimientos:

1) Conexión tanque: este consiste en conectar un tramo de tubería a untanque que contiene un mezclador a través de una conexión adiabática; talcomo se muestra a continuación:

mezclador

tramo de tuberìa conexiòn adiabàticatuberìa- tanque

La idea de este proceso consiste en utilizar el mezclador durante unintervalo de tiempo largo para que la temperatura en el fluido se vuelvahomogénea.

2) Mezclador estático: experimentalmente o en la práctica se coloca unmezclador estático formado por deflectores los cuales son superficiesalabeadas tridimensionales (no hay elementos motores).

mezclador estàtico

3) Numéricos: consiste en determinar experimentalmente U(r,x) y T(r,x)

para luego integrar numéricamente estas variables en la expresiòn de Tb.

Ecuación de Newton

Supongamos la siguiente situación:To

Tb

Ts

q” Tsup > T fluido

Donde: To..Distribución uniforme de temp. del fluido a la entrada. Ts..Temp. superficial de la tubería. Tb..Temp. volumètrica en esa sección. q”..Flujo de calor de la superficie hacia el fluido Tsup>Tfluido

De la ecuación de Newton, podemos cuantificar el proceso detransferencia de calor por convección, es decir:

qll .h T s T bAhora bien, realizando una equivalencia térmica entre el mecanismo de

convección y conducción asociado a la pared de la tubería se tiene que:

qll .k d

d rT

r R

.h T s T b.k d

d rT

r R

h

.k d

drT

r R

T s T bsi Nu

.h D

kNu loc

.d

d rT

r R

D

T s T bLa relaciòn anterior es conocida como el nùmero de Nusselt local (para

una tuberìa) debido a que està en funciòn de la temperatura volumètrica mediaTb, que como se sabe varìa con la posiciòn axial.

El nùmero de Nusselt se puede representar gráficamente de la siguientemanera:

Nu

x

Let

zona de completodesarrollo tèrmico

Nu(x)

zona asintòtica Nu.inf

1,05 Nu.inf

Del gràfico anterior se pueden resaltar los siguientes aspectos:1) Si x es igual a cero, es decir, cuando el fluido està entrando a la

tuberìa el nùmero de Nusselt local tiende a infinito. En otras palabras:si x 0 Nu loc ∞

Una vez que se determina Nuinf se multiplica por un factor de 1,05 esdecir (1,05 x Nuinf) para de esta manera conseguir la longitud de entradatèrmica Let.

En algunos casos, es necesario realizar un balance de calor entre lospuntos de una tuberìa, para esto, resul ta conveniente definir elnùmero de Nusselt de manera que pueda ser uti l izado comoconstante dentro de un determinado intervalo. De tal manera, sedefine el nùmero de Nusselt promedio como:

Nu.h D

k.1

xd

0

xxNu( )x

Donde Nu es funciòn del nùmero de Nusselt local .

Nu

x

Nu.pro

Nu.loc

2) La curva del número de Nusselt promedio esta siempre porencima de la del Nusselt local .

3) Cuando x t iende a infini to, el número de Nusselt promediotiende al nùmero de Nusselt local .

Balance de calor ( Anàlisis ingenieril )

Condición de temperatura constante (Ts=ctte)

r

x Hx Hx+dx

q”pdx

dx

2R

Ts

Ts

To

Suposiciones: i ) Ts=ctte i i) Ts>To i i i ) condiciones estacionarias. m=ctte

Cp=ctte1º Ley de la termodinámica para un sistema abierto:

q neto W H e H s 0

..qll p dx H x Hx dx 0 d

dx.H x dx ..qll p dx

si H x..m C p T b qll .h T s T b

..m C pd

d xT b

..h p T s T b

d

dxT b

..h p

.m C pT s T b

La relación anterior, es una ecuación di ferencial de primerorden lo que indica que se necesi ta de una condición de borde parapoder resolverla.

Condición de borde:En x 0 T b T o

Integrando ambos lados de la ecuación di ferencial por elmétodo de separación de variables se tiene que:

d

T o

T bT p

1

T s T b

..h p

.m C pd

0

xx1 ln T s T b ,T b T o

..h p

.m C px

Nota: h solo es constante en la zona de completo desarrollotérmico.

Si no se encuentra en la zona de completo desarrol lo térmico hdepende de x (h( x)).

dT o

T bT b1 .p

.m C pd

0

xxh( )x h .1

xd

0

xxh( )x

Luego para h variable se t iene que:

ln T s T b ,T b T o.

.h p.m C p

x lnT s T b

T s T o

..h p

.m C px

T s T b

T s T oe

..h p

.m C px

Nota: se debe conocer el número de Nusselt promedio paracalcular h promedio.

Correlaciones para tuberias circulares

Flujo Laminar

Hausen (1943) desarrollo la siguiente correlación semi-empírica, parala determinación del Número de Nusselt promedio.

3/2Pr]Re)/[(4,01

PrRe)/D(0668,066,3

k

D

D

DD

LD

LhNu

++==

<

>2000Re

05.0PrRe )/ (

D

DDL

Para tubos “cortos” la ecuación uti l izada es la recomendada porSieder y Tate (1936):

14,03/1 Pr]Re)/[( 86,1

k

D

==

sDD LD

hNu

µµ

<<<

>

16700Pr48,0

2000Re

10PrRe)/(

D

DLD

Propiedades a temperatura promedio, excepto sµ que se evalúa a sT

Flujo turbulento

La ecuación de Dittus-Boelter (Berkekey, 1930) ha sido ampl iamenteusada:

nDD

hNu Pr Re 023,0

k

D 8.0==

<<<<

>

160Pr7,0

10Re10000

10

6D

D

L

Donde n=0,4 para calentamiento y n= 0,3 para enfriamiento. Laecuación anterior es relativamente simple. Sin embargo, se puedetener errores de ± 20%.Petukhov (1970) presento una correlación mucho más exacta quecorrelaciona bien los datos experimentales de muchos investigadores:

n

s

DD

f

fhNu

−+

==µµ

)1(Pr 8/ 7,1207,1

PrRe)8/(

k

D

3/2

<<<<

>

2000Pr5,0

105Re10000

10/6x

DL

D

n= 0.11 para calentamienton= 0.25 para enfriamienton=0 para gases

La ecuación anterior incluye el factor de fr icción, el cual puedeobtenerse del diagrama de Moody o bien mediante la ecuación deChurchi l l (1977)

12/1

2/3

12

)(

1

Re

8

8

++

=

BA

f

D

16

9,0 27,0)Re/7(

1 ln 457,2

+=

D

eA

D

16

Re

37530

=

D

B

Gnielinski (1976) modif ico la ecuación de Petukhov para ampl iar elrango de números de Reynolds y propuso una ecuación de la forma:

)1(Pr 8/ 7,121

Pr)1000)(Re8/(

k

D

3/2 −+−==

f

fhNu D

D

<<<<

>

2000Pr5,0

105Re2000

10/6x

DL

D

Ejemplo 3.2 Agua fluye a una temperatura promedio de 30 °C y a unavelocidad de 1m/s por una tubería de diámetro interno de 2,5 cm. Lasuperficie de la tubería es mantenida a 50 °C. Determinar elcoeficiente de transferencia de calor usando la ecuación de(a)Petukhov, (b) Di ttus-Boelter

Solución

A Tb= 30 C y Ts= 50 C, las propiedades del gas son:

smvmsKg /10 8012,0, / 10 7978,0 2-63 == −µ

42,5Pr, / 6150,0 == mCWk

msKgs /10 5471,0 3−=µ

así,

10 12,310 8012,0

025.0 1Re 4

6x

x

xD == − ( turbulento)

(a) Ecuación de Petukhov

Considerando que la tubería es l isa (e=0), se determina el factor defricción, por el diagrama de Moody o por la ecuación de Churchil l .

Así

023,0 =f

susti tuyendo en la ecuación de Petukhov:

206)1(Pr 8/ 7,1207,1

PrRe)8/(

k

D

3/2=

−+

==n

s

DD

f

fhNu

µµ

CmWxDkNuh D2/ 5066025.0/6150,0206/ ===

(b) Ecuación de Dittus-Boelter

Este úl t imo valor di f iere en 14% con relación a la ecuación dePetukhov.

1,178PrRe023,0k

D 4.08.0 === DDh

Nu

CmWxDkNuh D2/ 4381025.0/ 6150,0 1,178 / ===

Heat Transfer

Documents

Transcript of Heat Transfer