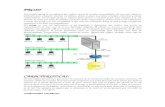
Magnetmetro SQUIDAlejandro Bartel , Juan Pablo Garca GutirrezTutor: Daniel Slomovitz Departamento de Medidas Elctricas, Instituto de Ingeniera Elctrica, Universidad de la Republica, Montevideo, Uruguay En este artculo vamos a explicar el funcionamiento de los dispositivos denominados magnetmetros SQUIDS que son capaces de medir campos magnticos muy pequeos y trataremos un ejemplo concreto de su aplicacin en la medicina en donde aprovecha esta propiedad. Estudiaremosel tema desde el punto de vista de la mecnica cuntica introduciendo los conceptos bsicos que permitan el entendimiento y anlisis de estos dispositivos tanto a nivel macroscpico como microscpico. ..I. INTRODUCCIN E l SQUID[1]es uno de los dispositivos superconductores ms utilizados.Este es un detector extremadamente sensible a los cambios deintensidaddel campomagntico. Seutiliza tantoenaplicaciones militarescomomdicas. Escapazde detectar seales elctricas del cerebro y el corazn con gran precisin. Puede comprobar el buen estado de tuberas y puentesdemaneranodestructiva. Seutilizatambinenel paleomagnetismo, sensores geolgicos para prospecciones petrolferas. Equipos militares de deteccin de submarinos observando los cambios que stos producen en el campo magnticode laTierra cercanoaellos. Observacinde la circulacin de la sangre ya que la sangre posee propiedades magnticas cuandoseleponecercadeunvasosanguneo, etctera.ElSQUIDpuedeutilizarse comounmagnetmetroextre-madamente sensible, ya que es posible detectar un cambio de flujo magnetico,mas pequeo que un fluxon (unidad elementalde flujo magntico cuntico) Existen dos tipos de SQUIDS el de corriente directa y el de radiofrecuencia. En la figura 1 se muestra un esquema de cmo est conformado un SQUID de corriente directa. I I. UN POCO DE FSICA CUNTICAEl trmino "mecnica cunticafue utilizado por primera vez por Max Born en 1924.Esla fsica que estudia la materia a escala atmica. Surge en el siglo XX y rompi con todos los paradigmas de la fsica que haban prevalecido hasta ese entonces. La fsica cuntica respondeaciertas ocurrencias probabilsticassobreelcomportamientodelostomosdela materia.Lafsica cuntica surgedelaimposibilidaddela mecnica clsica para explicar fenmenos a una escala atmica; a ese nivel los fenmenos tienen la caracterstica de ser estudiados por necesidad en trminos probabilsticos; dado quelaspartculas enestudiosontanpequeas, queel solo hecho de observarlas altera el fenmeno observado, por lo que nosepuedeconocer conexactitudentrminos clsicos su posicinyvelocidadal mismotiempo, por ejemplo. Delo anterior surgen ecuaciones de onda en donde las variables para definir el comportamiento de estas partculas se expresan en trminos de probabilidades. II.1)MODELO ATMICO ACTUAL YLA ECUACIN DE ONDA [2]Detodaslassuposicionesyteoras hechasacercade la representacindel modeloatmicolasqueprevalecenenla actualidad son las siguientes:1). Lapresenciadeun ncleo atmico con las partculas conocidas (protones, electrones,) la casi totalidad de la masa atmica en un volumen muy pequeo.2). Los estados estacionarios o niveles de energa fundamentalesenlos cualessedistribuyenlos electrones de acuerdo a su contenido energtico. 3). La dualidad de la materia (carcter onda-partcula). En el caso de partculas pequeas (electrones) lalongituddeondatieneunvalor comparable con las dimensiones del tomo.4)Laprobabilidadenunlugar decerteza, en cuanto a la posicin, energa y movimiento de un electrn.Erwin Schodinger, fue el que propusoel modelo atmicoactual, llamadoEcuacin de Onda, una frmulamatemticaqueconsideralosaspectos 1 Figura 1 Esquema del SQUIDanteriores. Lasolucindeestaecuacin, es la funcin de onda (), lo cual es una medida de la probabilidad deencontrar al electrn en el espacio. En este modelo, el rea donde hay mayor probabilidad de encontrar al electrn se denomina orbital. Se trata de una ecuacin diferencial que para el caso ms sencillo en el que consideramos la propagacin de la onda en una sola direccin presenta la forma:

(1)Donde m es la masa del electrn, h la constante de Planck y V es un potencial aplicado a la partcula.[2]As sefundunanuevamecnica, lade las partculas atmicas, que se llamo mecnica cuntica. El trmino cuntico viene al caso, porque generalmente, la ecuacin de Schrodinger solo tiene solucin para determinados niveles de energa. Es decir, la cuantificacin de la energa, aparece como algo natural en la mecnica cuntica.Mostraremos un ejemplo en el que basaremos nuestro estudio del funcionamiento del Squid. Mostraremos la solucin de la ecuacin de onda con las siguientes condiciones de borde: Para resolver la ecuacin (1) con las condiciones de borde de arriba vamos a asumir que el potencial V es independiente del tiempo, en este caso la ecuacin de Schrodinger puede ser resuelta por el mtodo de separacin de variables. Buscamos soluciones de la forma donde es una funcin solo de x yes una funcin solo de t. Para soluciones separables se tiene que:yla ecuacin total queda entonces y dividiendo todo entre queda ahora el lado izquierdo es una funcin solo de t y el lado derecho es solo una funcin de x entonces ambos lados de la igualdad son una constante . Llamaremos entonces a esa constante E, o entoncesoLa separacin de variablesha transformado a la ecuacin diferencial parcial(1)en dos ecuaciones diferenciales ordinarias (ecuacin(7) y (9) ). La primera de las dos es fcil de resolvery su solucin bien conocida espero podramos absorber la constante C enluego LasegundaecuacinesllamadalaecuacindeScrodringer independiente del tiempo y para resolverla necesitamos que la funcinV(x) sea especificada, enel ejemplodel potencial infinito V(x) es definida en la figura (2).En el ejemplo a desarrollar la partcula es completamente libre excepto en los extremos (x=0 y x=a) donde existe una fuerza infinita que no la deja escapar. Fueradel pozo( la probabilidad de encontrar a la partculaenesazonaes0). Dentrodel pozodondeV=0la ecuacin de Schodringer independiente del tiempo queda:(11)(12) donde Laconstante k estabien definidapues E espositivoya que E>V(ver Anexo) yVes 0enel ejemploque estamos analizandoLaecuacin(12)esladeunoscilador armnico simple, y la solucin general es: donde A y B son constantes arbitrarias quesefijaranconlascondiciones deborde. Las condiciones de borde para se basan en la continuidad de llll yaunque como el potencial va a infinito solo la primera se cumple. La continuidad deimplica lo siguiente y evaluandoenenx=0 y x=a obtenemos: por lo queB=0entoncesnosvaquedando: Ahora evaluando en x=atenemos:de donde se desprende que A=0 (en la que caemos en la solucin trivial no normalizable y sin sentido fsico) sin(ka)=0la cual impone que la solucin que se desprende de tomar k=0 es nuevamente la solucin nula, y las soluciones negativas no aportan nada nuevo dado que ,. , y podemos entonces absorber el signo de menos en la constante A. Entonces los posibles valores de k son:

Falta determinarelvalorde laconstante A, pero antescabe mencionarquelos posibles valoresde k dejan determinados posibles valores de E pues: (13)A diferencia de la mecnica clsica, la partcula en el pozo de potencial infinito no puede adquirir cualquier cantidad de energa sino que solo esos especiales valores permitidos.Fijemos ahora la constante A , esta surge de la normalizacin de la funcin de onda en el sentido de que la probabilidad de 2 Figura 2 Esquema del potencial V(x)encontrara lapartcula entodo el espacio es 1, por lo que tenemos:(14)Despejando se tiene que Entonces dentro del pozo las soluciones quedan:(15)Estas conforman un conjunto infinito de soluciones, una para cada entero n. En la figura (3) se muestran graficadas las soluciones para n=1, n=2 y n=3 respectivamente. ,es es el que posee la energa mas baja y es llamado estado tierra, los otros armnicoscuya energa se eleva de forma proporcional a n2 son llamados estados excitados . Como grupo las funciones tienen interesantese importantes propiedades. Algunas de ellas son las que se enumeran:1) Ellas son alternadamente par e impar con respecto al centro del pozo (es par , es impar ,es par y asi sucesivamente.2) Cuando se aumenta la energa, cada estado sucesivo tiene un nodo mas (cruces por cero). .no tiene ninguno (el punto inicial y final no cuentan)tiene uno ytiene 2 y as sucesivamente.3) Ellas son mutuamente ortogonales en el sentido de : 4) Ellas forman un espacio vectorial completo, en el sentidode que cualquier funcinh(x)puede ser escrita como una combinacin lineal de ellas: h Los estados estacionariosde la ecuacin de Scrodinger para el pozo de potencial infinito quedan entonces:

(16)Sabiendo que para cada estado permitido hay una ecuacin de onda es decir :

(17)Obtenemos para nuestro caso el siguiente resultado: (18) El cual conociendo la ecuacin en el instante inicial podemos mediante Fourier obtenerlos coeficientes de la siguiente forma: (19)Otro ejemplo que no estudiaremos aquiesla barrera finitaX < -a => V0= 0-a< X < a =>-< -V0< 0X > a => V0= 0Esto se conoce como la barrera finita, en este caso, la funcin de onda existe en las tres regiones. Esto significa que hay cierta posibilidad de que una partcula con E < V, atraviese la barrera. Esto se conoce como EFECTO TUNEL.II.2) SUPERCONDUCTORES Y PARES DE COOPER[3]Lasuperconductividadesunfenmenoquebsicamente comprende el estado en el cual la resistencia elctricade ciertos materiales disminuye de forma repentina hasta llegar a cero. La temperatura por debajo de la cual la resistencia elctrica de un material se aproxima a cero absoluto se denomina temperatura de transicin crtica (Tc). Por encima de esta temperatura, al material se lo conoce comonormal, y por debajo de Tc, se dice que es superconductor, en lafigura (4) semuestra lareginde superconduccinde algunos materiales delimitada por la curva caracterstica B-T de los mismos. Se presentan tambin efectos magnticos notables: la permeabilidad del material disminuye hasta cero y el flujo magntico en el material desaparece; la conductividad trmica aumenta rpidamente. Adems de la temperatura (T), el estado superconductor tambin depende de otras variables, como son el campo magntico (B) y la densidad de corriente (J). La superconductividad depende del campo magntico, dadoquesi seaplicauncampomagnticosuficientemente intenso a un superconductor a cualquier temperatura que est pordebajodesutemperaturacrtica(Tc), elsuperconductor retorna a suestado normal. El campo magntico aplicado necesario para restablecer la conductividad elctrica normal en el superconductor se denomina campo crtico (Bc). A densidad de corriente constante, la curva de Bcfrente a la temperatura, T (K), puede aproximarse mediante la expresin emprica: 1]1

,_

21co cTTB B(20)Donde Boes el campo crtico a una temperatura T=0 K, obtenido por interpolacin.La curva definida por la ecuacin (20) queseilustraenlafigura(4)representael limiteola frontera entre los estados normal y de superconductividad de un material superconductor.

3Figura 3 Esbozo de las soluciones para primeros armonicosVQu es lo que hace que un superconductor pierda su resistencia? Parece razonable que a temperaturas muy bajas, la estructura atmica del material presente una forma perfectamente ordenada por la cual los electrones pueden moverse por elespacio vacoentrelosncleos atmicos sin chocar con nada ni perder energa. Pero en realidad el fenmeno fsico es ms complejo. Los electrones que intervienen en la superconductividad se presentan en la forma conocida como pares de Cooper, con movimiento de rotacin o spin en sentidos opuestos. Una de las razones de la superconductividad sera el movimiento concertado y ordenado de estos pares de electrones. En un conductor normal los electrones encuentran obstculos para viajar debido a la agitacin trmica y a la distorsin de la red metlica, pero amuybajastemperaturas, laagitacintrmicadesaparecey los electrones pueden adaptarse a las distorsiones de la red si viajanatravsdeelladeapares. Entodos losmateriales superconductores sehaobservadoquelacorrienteelctrica est conformada por pares de electrones;es decir que ya no son partculas individuales las que recorren el conductor, sino que hayunmecanismoque hace que estas partculas, que normalmente se repelen ya que poseen la misma carga, queden ligadas. Es precisamente estaenergadeligaduralaquele permite a los electrones superar los obstculos que normalmente provocaran su dispersin.Podemos describir este fenmeno de la siguiente manera: el electrn superconductor al pasar cerca de un ncleo atmico (con carga positiva) lo atrae, generando una regin de carga positiva alrededor de l; se forma as una nube electrnica que permite que otro electrn (con carga negativa) sea atrado y se forme el par (llamadopar de Cooper), de esta manera, el ncleo del tomo acta como mediador en esta interrelacin de atraccin entre dos electrones, en la figura (5) se ilustra este fenmeno. Si ahoralatemperaturasubepor arribadelade transicin, el material adquiere suficiente energa trmica para que las vibraciones en su estructura rompan los pares,y por tanto vuelva a aparecer la resistencia.II.3) JUNTURA TUNEL Y EFECTO JOSEPHSON[4]El efecto tnel electrnico se puede describir observando la figura (6) en donde se muestranlos diagramas de niveles de energa de dos metales normales.Lazonareyadarepresentaestados electrnicos yaocupados por los electronesen cada metal. La parte blanca muestra los estados disponibles. Atemperatura cero, el paso de los electrones de un metal a otro queda completamente prohibido porelprincipiodeexclusindePauli. Cuandoseaplicaun voltaje positivo al metal de la derecha, de manera tal que los niveles de energa deE, ya no coinciden, hay estados ocupados enel metal de la izquierda al mismonivel que estados desocupados en el metal de la derecha y el efecto tnel puede ocurrir, como se indica por las flechas. Es evidente que el nmero de estados que quedan disponibles para el proceso dependendel voltaje aplicado, ysi el efectode tunel es constante, como ocurre por voltajes aplicados muy pequeos, la corriente resultante vara linealmente con el voltaje aplicado. Cuandolos dos superconductores estnseparados por una capa de unmedioaislante ounmetal nosuper- conductor de unos pocos nanmetros, los pares de Cooper puedenatravesar labarrera por efectotnel, Aunque los pares de Cooper no pueden existir en un aislante o un metal no superconductor, cuando la capa que separa los dos superconductores es lo suficientemente estrecha, estos la pueden atravesar y guardar su coherencia de fase. Es la persistencia de esta coherencia de fase loque dalugar al efectoJosephson.Las ecuaciones bsicas3quegobiernanla dinmica del efecto Josephson sonLas ecuaciones bsicasque gobiernan la dinmica del efecto Josephson son:(21)donde U(t) e I(t)son los voltajes y la corriente a travs de la unindeJosephson,(t)es ladiferencia defaseentre las funciones de onda en los dos superconductores que forman la unin, e Ic es una constante, la corriente critica de la unin. La corriente critica es un parmetro experimental importante del dispositivo que puede alterarse tanto por la temperatura como por un campo magntico aplicado. La constante fsica, h/2e es el cuanto de flujomagntico, la inversa del cuales lacons- tante de Josephson.IIIMAGNETOMETRO SQUIDFigura 4Variacin del campo magntico B con latemperatura Ten un material superconductor para distintas sustancias.4Figura 5 Formacin de pares de Cooper en un material superconductorFigura 6Niveles de energia de 2metales diferetesYa introducidos los conceptos bsicos de la mecnica cuntica podemos proceder conelfuncionamientodedeteccinde campos magnticos con el SQUID.[5]Las lneas de campo magntico que pasan a travs de el centro del circulo superconductor provocan corrientes en el Squid determinando las fases de las ondas de los pares de Cooper. Se crea as una nueva onda (interferencia de las ondas anteriores) cuyomoduloesproporcional al flujomagntico sobre el anillo. Como los superconductores no tienen resistencia elctrica la interferencia puede ser medida solo interrumpiendo al superconductor con pequeas regiones que ofrezcan resistencia elctrica, este ser el papel de las 2 junturas Josephson en las cuales se generara a travs de ellas ladiferenciadepotencial. El voltajemedidoatravsdelas junturas es proporcional al flujo magntico sobre el Squid.[5] Al hablar del flujo de una corriente superconductora hay que considerar la coherencia de fase, que es una consecuencia del hecho de que los pares de electrones no pueden ser dispersados. La funcin de onda de electrn libre en un metal es igual a:

(22)donde la fase de la onda es k r y r es la posicin de la onda en el espacio respecto a un referencial fijo.Cada vez que un electrn es dispersado, el vector de onda krcambia yestodalugar aque cuandounelectrnlibre se mueve a travs de un metal, su kr experimenta muchos cambios, demanera quesufuncindeondaexperimentar muchos cambios de fase aleatorios Esto es distinto en el caso de un superconductor. La funcin de onda ir ahora asociada a un par de electrones, y el kr de la funcin de ondas ser el kr efectivocombinadodelosdoselectrones. Paralosparesde electrones superconductores no existe dispersin,es decir, su kr efectivo no cambia. Por eso, la diferencia de fase entre dos posiciones r1yr2ser k(r2- r1) cualquiera que sea la distancia r2- r1 Esto es lo que se entiende porcoherencia de fase. Una consecuencia de la coherencia de fase es la cuantizacin del flujo. Consideremos un anillo superconductor de radio R con una determinada cantidad de flujo magntico, , ensuinterior.El flujomagnticoest causado por corrientes persistentes en la superficie del anillo. [7] En cualquier punto de la circunferencia interior ha de haber coherencia de fase, es decir: (23)Buscamos una relacinentre k, la densidad de corriente superconductora js y el flujo . La cantidad de movimiento de un electrn libre es:

(24)En presencia de un campo magntico:

(25)Donde m ,e y v son la masa, carga y velocidad de un electrn respectivamente yA es el vector denominado potencial vector . Por lo tanto para un par electrnico la cantidad de movimiento es igual a: (26)y la densidad de corriente superconductora

(27)(con ns: densidad de electrones apareados).Despejando k de las ecuaciones (26) y (27) llegamos a que el vector de onda del par de Cooper es (28)Integrando alrededor de la circunferencia de radio R,(29)Aplicando el teorema de Stokes y sabiendo que B = rot A(30) Utilzando adems laecuacin de London

(31)Tenemos que:(32)(33) (34)Ypor lotantoel flujoesta cuantizado. Hayquetener en cuenta que lo que nos interesa en realidad es elext ya que con el podremos obtener la medida del campo magntico externo. Se prueba experimentalmente que elint VminDado d2dx2 = 2m 2 [V (x) 'E] i,si E