717

11SOLUCIONARIO

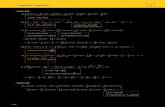
125 Calcular la integral # ln x

xdx

2.

(Castilla y León. Junio 2008. Prueba A. Problema 2)

u x dux

dx

dvx

dx vx

ln1

1 12

 

 

F

ln ln ln lnx

xdx

x

x xdx

x

x xk

x

xk

2 2

1 1 1

PREPARA TU SELECTIVIDAD

1 Dada la función f xx

x5 42:

a) Calcula la integral #f x dx( ) . b) Halla la primitiva F de f que cumple que F(1) 1.

(Cataluña. Septiembre 2005. Cuestión 2)

a) F x f x dxx

x

dxx

x

dx x( () )5 4

1

10

10

5 4

1

55

2 2

2 4 k

b) F(1) 1 → 1

51

4

5k k → F x x( )

1

55 4

4

5

2

2 Determina f ( x ) sabiendo que f x x f f f'" " '( ) ; ( ) ; ( ) ( )24 0 2 0 1 0 0y .

(Castilla-La Mancha. Junio 2005. Bloque 1. Pregunta B)

f x x f x x dx x k''' ''( () )24 24 12 21

Como f k f x x'' ''( ) (0 2 2 12 212)

f x x f x x dx x x k'' '( ( ( )) )12 2 12 2 4 22 2 32

Como f k f x x x' '( ) (0 1 1 4 2 123)

f x x x f x x x dx x x x k'( ( ( )) )4 2 1 4 2 13 3 4 233

Como f k f x x x x( ) ( )0 0 034 2

3 Sea f : R → R la función definida por f x x ex( ) ( )1 2. Calcula la primitiva

de f cuya gráfica pasa por el punto (1, e2).

(Andalucía. Año 2004. Modelo 3. Opción B. Ejercicio 2)

u x du dx

dv e dx v ex x

1

F

F x x e dx x e e dx x e e kx x x x x( ( ) ( ) ( )) 1 1 1 (( )x e k

x2

F e e k e k e e F x x e e ex( ) ( ( )1 22 2 2 2)

718

Integrales indefinidas

4 Dada la función f : [1, e] → R definida por f xx

x( ) ln1

, calcúlese una función

primitiva de f ( x ) que pase por el punto P(e, 2).

(Castilla y León. Septiembre 2004. Prueba B. Problema 2)

u x dux

dx

dv dx v x

ln1

 u x du dx

F

F xx

x dxx

dx x dx x( ln ln ln)1 1

xx x x kln

F e k k F x F x x x x x( ) ( ( ln ln2 1 2 1 1) )

5 Dada la función f : R → R definida por f ( x ) Ln (1 x2), halla la primitiva de f cuya

gráfica pasa por el origen de coordenadas (Ln denota la función logaritmo neperiano).

(Andalucía. Junio 2007. Opción B. Ejercicio 2)

u x dux

xdx

dv dx v x

ln ( )12

1

2

2

F

F x x dx x xx

xdx( ln ( ) ln ( )) 1 1

2

1

2 22

2

x xx

dx x xln ( ) ln ( )1 22

112

2

2 22 2x arc tg x k

F k F x x x x arc tg x( ) ( ) ln ( )0 0 0 1 2 22

6 Hallar una primitiva de la función f ( x ) x ex.

(Extremadura. Junio 2006. Repertorio B. Ejercicio 2)

u x du dx

dv e dx v ex x

F

xe dx xe e dx xe e kx x x x x

7 Calcula la siguiente integral: # x

xdx

( )1 3

(Castilla-La Mancha. Septiembre 2007. Bloque 2. Pregunta A)

x

xdx

x xdx

( ) ( ) ( )1

1

1

1

1

13 2 3 (( ) ( )x x

k1

1

2 1 2

8 Resolver # 2

3 33 2

x

x x xdx .

(Canarias. Septiembre 2006. Opción A. Cuestión 1)

2

4 3

1

1

3

32

x

x xdx

x xdx xln 11 3 3ln x k

719

11SOLUCIONARIO

9 Calcular la primitiva que sigue:

# x x

xdx

3 2

2

1

4

(País Vasco. Julio 2007. Bloque D. Cuestión D)

x x

xdx x

x x

3 2

2

1

41

13

4

1

2

3

4

1

2dx

xx x x k

2

2

13

42

3

42ln ln

10 Calcule # x

x xdx

5

4 32.

(Galicia. Junio 2008. Bloque 3. Opción 2)

x

x xdx

x xdx x

5

4 3

2

1

1

32

2ln 11 3ln x k

11 Utilizando el cambio de variable t ln x, calcular # ln (ln )

ln

x

x xdx .

(Aragón. Septiembre 2006. Opción B. Cuestión 2)

t x

dtxdx

ln

1

F

ln (ln )

ln

ln (ln ) (ln (ln ))x

x xdx

t

tdt

tk

x2 2

2 22k

12 Dados a y b dos números reales, calcula la integral indefinida:

# sen x

a b cos xdx

( )2

Presta atención a las posibilidades a 0 o b 0.

(La Rioja. Septiembre 2004. Propuesta B. Ejercicio 5)

Si a 0 y b 0: senx

a bcos xdx

b a bcos xk

( ) ( )2

1

Si a 0 y b 0: senx

bcos xdx

bcos xk

2

1

Si a 0 y b 0: senx

adx

cos x

ak

2 2

a y b no pueden ser 0 simultáneamente, pues no existiría la función

que tenemos que integrar.