Enginyeria Industrial

ETSEIB - UPC

CALCUL NUMERIC i SIMULACIO

Practiques

Curs 2004–2005

Antoni Susın

1

Capıtol 0

Llenguatge i eines grafiques

El paquet en que programarem les practiques de l’assignatura de Calcul Numeric i Simulacioes el Matlab. No es suposa coneixement previ de Matlab i per aixo es dedicaran unes sessionsinicials a la introduccio d’aquest programa. Suposarem coneguts una serie d’aspectes de laprogramaci3

4que ja s’han vist a les assignatures d’Informatica, com ara els diferents tipus

de variables, operadors, estructures de control de flux, etc. Al llarg del curs farem emfasi enels aspectes que mes ens interessin des d’un punt de vista de calcul numeric.

Tambe utilitzarem tota la potencia de la representacio grafica dels resultats que permetel Matlab.

3

4 CAPITOL 0. LLENGUATGE I EINES GRAFIQUES

0.1 Exemples Inicials amb Matlab

En el primer exemple podem veure com s’introdueix una matriu pel teclat i com es podemfer algunes operacions elementals amb matrius.

% ==========================> EXEMPLE 1 <===========================

% Definicio d’una matriu des d’el teclat

A=[1 2; 3 4; 5 6]

%Definicio d’una matriu amb una comanda predefinida

identidad= eye(3)

% Operacions amb matrius

B=A’; % B es la transposada de A

% C=A+B; % suma (error)

% D=A*A % producte (error)

E=A*B; % producte

N=[1 2 1; 3 4 1; 5 6 0] % nova matriu

F=inv(N); % inversa

F*N % comprovacio

pause

% Resoluci\’o d’un sistema d’equacions lineals

clear all; % neteja l’espai de treball

A=[4 -5 3; 1 2 1; 1 -1 -4]; % matriu de coeficients

b=[31; 8; 3]; % vector de termes independents

x=inv(A)*b; % calcul del vector de incognites

xx=A\b; % una altra forma

%--------------------------------------------------------------------

En el segon exemple podem veure com treballar amb polinomis dins el Matlab. Opera-cions com l’avaluacio d’un polinomi, el calcul dels seus extrems, etc.

0.1. EXEMPLES INICIALS AMB MATLAB 5

% ========================== EXEMPLE 2 ===========================

% Volem calcular les arrels d’un polinomi de quart grau

% Tambe es vol saber quin valor pren el polinomi quan x es igual a 1 i

% quan x es igual a alguna de les arrels trobades en el pas anterior (comprovacio).

% A continuacio tambe es vol saber en quin valor de x hi ha extrems absoluts o

% relatius (maxims o minims) i el valor dels mateixos. Para aixo es calculara la

% derivada de P(x) i s’obtindran les arrels del polinomi resultant. Aquests

% s’hauran de substituir en P(x) per coneixer el valor en els extrems.

pol = [1 -9 31 -59 30]; % introduccio del polinomi P

xraiz = roots(pol); % calcul de les arrels

polyval(pol,1); % avaluacio del polinomi en x=1

polyval(pol,xraiz(1,1)); % avaluacio del polinomi en una de les arrels trobades

der = polyder(pol); % derivem el polinomi

xderraiz = roots(der); % calculem les arrels de la derivada

polyval(pol, xderraiz(1,1));% avaluem el polinomi en els seus extrems

segder=polyder(der); % segona derivada

plot([0:0.01:8],polyval(pol,[0:0.01:8])), grid on % grafica de la funcio

%--------------------------------------------------------------------

A continuacio donem un exemple sinusoide.m en el que es dibuixa la grafica de la funciosin(x) i permet fer-ne una animacio.

%==================> EXEMPLE 3 <========================

% Animacio d’una sinusoide sin(x+F)

% la fase F es el parametre d’animacio

%

endF=2*pi; %valor maxim de variacio de l’angle de Fase

incF=0.05; %increment de la Fase

%Assignem la finestra de dibuix a la nostra aplicacio

6 CAPITOL 0. LLENGUATGE I EINES GRAFIQUES

Figura 1: Representacio de la funcio sin(x)

figNumber=figure( ...

’Name’,’Animacio d’’una sinusoide’, ...

’NumberTitle’,’off’, ...

’Visible’,’on’);

x=[-2*pi:0.2:2*pi];%-incx];

for F=-endF:incF:endF

y=sin(x+F);

plot(x,y,’r’)

axis([-2*pi 2*pi -1.2 1.2])

grid

line([-2*pi 2*pi],[0 0],’Color’,’k’,’LineWidth’,2)

line([0 0],[-1.2 1.2],’Color’,’k’,’LineWidth’,2)

text(1.15,1.1,[’Fase = ’ num2str(F,’%.4f’)])

0.1. EXEMPLES INICIALS AMB MATLAB 7

drawnow

%pause(0.01)

end

%--------------------------------------------------------------------

8 CAPITOL 0. LLENGUATGE I EINES GRAFIQUES

Capıtol 1

Aplicacio Logıstica

1.1 Iteracio grafica de l’equacio logıstica

Considerem la iteracio definida per l’equacio:

xn+1 = λxn(1− xn), xn, λ ∈ R, (1.1)

on cal prendre un valor inicial x0, i λ es un valor fixat. La representacio grafica d’aquestaiteracio consisteix en el proces que descriurem a continuacio.

Si considerem, en general, una funcio d’iteracio xn+1 = f(xn), veiem que el valor de lesabscisses i les ordenades s’intercanvia a cada pas. Aquest proces es pot representar utilitzantels punts de la bisectriu del primer quadrant, de manera que la representacio grafica d’unaiteracio consisteix en una poligonal que uneix successivament punts sobre la grafica de lafuncio d’iteracio i punts sobre la bisectriu. Aixı, si partim de x0 (punt (x0, 0) ) i calculem elvalor de x1 (punt (x0, f(x0)) ), farem la recta que uneixi aquests dos punts i la continuaremde manera horitzontal fins a tallar la bisectriu (punt (x1, x1) ). Despres calcularem el seguentiterat x2 = f(x1) i unirem el punt anterior de la bisectriu amb aquest nou punt (x1, x2), irepetirem el proces un nombre finit N (prou gran) de vegades.

Normalment el que es preten estudiar es el comportament lımit de la successio (xn)n∈N , iveure com depen aquest dels diferents parametres de la iteracio. En el nostre cas estudiaremel comportament en funcio del valor inicial x0 i de λ.

Exercici 1.1.1 A partir de l’exemple de representacio de la funcio f(x) = sinx, feu larepresentacio dels eixos, la bisectriu i la funcio d’iteracio logıstica 1.1 per λ = 2.8, dins lafinestra d’extrems (-0.3,-0.3) i (1.3,1.0).

9

10 CAPITOL 1. APLICACIO LOGISTICA

Exercici 1.1.2 Per N = 200 i λ = 2.8 representeu les iteracions per diferents punts inicialsx0. Feu que el programa demani x0 per teclat i experimenteu amb diferents valors, perexemple 0.1, 0.2, 0.4, 0.6, 0.8, 0.9 (Obs. Que passaria si prenguessim x0 = 0?).

Posteriorment feu l’animacio pels valors de λ entre 1.5 i 4.0 amb pas ∆λ = 0.05 prenentsempre N = 200 i x0 = 0.9

−0.2 0 0.2 0.4 0.6 0.8 1 1.2−0.2

0

0.2

0.4

0.6

0.8

Param = 2.8000

Figura 1.1: Grafica de l’aplicaco logıstica per λ = 2.8

1.2 Diagrama de bifurcacions de Feigenbaum

Ara volem posar de manifest la variacio en el comportament final de l’equacio logısticaen variar el parametre λ. Per aixo farem el que s’anomena diagrama de bifurcacions deFeigenbaum, que s’obte al variar els diferents valors de λ i representar nomes els valors lımit

1.2. DIAGRAMA DE BIFURCACIONS DE FEIGENBAUM 11

de les successions d’iteracio. Aquest es l’exemple mes senzill en el que podem trobar uncomportament caotic en el comportament d’una iteracio.

Exercici 1.2.1 Feu el diagrama de bifurcacions de Feigenbaum, que s’obte al variar elsdiferents valors de λ i representar nomes els valors lımit de les successions d’iteracio.

Fixeu N = 200, finestra de dibuix amb eixos (x, λ) i valors (−0.3, 2.8) i (1.3, 4) respecti-vament per als seus extrems. Prenem sempre un punt fixat x0 = 0.9, i per a cada valor deλ iterem aquest punt inicial. Donat que ens interessa el comportament en el lımit, podemrepresentar nomes els punts (xn, λ) a partir de n = 50 (per evitar el soroll inicial). Aquestproces el repetirem des de λmin = 2.8 fins a λmax = 4 fent 300 subdivisions.

−0.2 0 0.2 0.4 0.6 0.8 1 1.22.8

3

3.2

3.4

3.6

3.8

4

Figura 1.2: Cascada de bifurcacions de Feigenbaun

12 CAPITOL 1. APLICACIO LOGISTICA

Capıtol 2

Aplicacio Estandard

2.1 L’aplicacio “estandar”

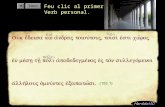
Amb aquesta practica volem obtenir una representacio del comportament caotic d’un sistemadinamic. Entendrem per sistema dinamic un cert mecanisme que permet seguir l’evolucio(o trajectoria) d’un cert valor inicial. El comportament caotic d’un sistema es manifesta enla gran diferencia entre els valors finals que s’obtenen en variar lleugerament els valors delsparametres que poden intervenir en el sistema.

Un exemple d’aquest tipus de sistemes ens el dona l’aplicacio estandar, que es una iteraciodels punts del pla R2. De fet, es una iteracio que podem definir com

{

yn+1 = yn +K sin(xn),xn+1 = xn + yn+1 mod(2π).

1. Preneu una finestra de dibuix centrada en el punt (π, π) de 2π de costat. Considereucom a valors inicials els punts situats sobre l’eix x = π, que recorrerem amb pas h = 2π

30.

2. Fixant un valor K = 1.11, per a cada punt inicial pinteu tots els punts de la seva orbita(els seus iterats) fins a n = 300 iteracions. Feu el mateix prenent ara els valors inicialssobre l’eix y = π.

3. Repetiu el calcul anterior pero per a valors de K ∈ (0.8, 3.4). Feu una sequenciaanimada que passi de K = 0.8 a K = 3.4, amb un pas de 0.2.

4. Repetiu l’animacio anterior prenent ara un pas de 0.1 per als valors de K i prenent

13

14 CAPITOL 2. APLICACIO ESTANDARD

una finestra de dibuix centrada en el punt (π, π) de 0.5 de costat (farem un zoom del’anterior).

Feu la practica en un arxiu que es digui standard.c.

Aplicacio estandar corresponent al nivell d’energia 0.08

Capıtol 3

Zeros de Funcions

3.1 Zeros de funcions

Volem calcular els zeros d’una certa funcio f(x) dins un interval [a, b]. El procedimentque seguirem es, en primer lloc, separar els possibles zeros (considerant que la funcio siguicontınua) fent un escombrat de l’interval d’estudi i detectant possibles canvis de signe. Unavegada determinat el subinterval en el qual hi ha un zero, aplicarem algun dels metodes decalcul de zeros. En aquesta practica, el que farem es calcular per duplicat els zeros, perpoder fer un estudi comparatiu de les diferents velocitats de convergencia dels metodes deNewton i de la secant.

Exercici 3.1.1 Considerem la funcio f(x) = 2x − ln x − 4 dins de l’interval [0, 4]. Volemconeixer els seus zeros amb una precisio tol<1.e-12.

• Dibuixeu la grafica de la funcio f(x).

• Calculeu els seus zeros pels metodes de Newton i la secant. Si el canvi de signe corresponal subinterval [ak, bk], preneu aquests valors com a inicials en el cas de la secant i preneuak com a valor inicial en el cas de Newton.

Doneu els resultats en un fitxer de resultats que anomenarem zeros.out cada una de lesiteracions necessaries per a calcular el zero corresponent amb els dos metodes. Per uni-formitzar, a cada lınia podeu escriure tres valors: un valor int corresponent a la iteracio,un double que sigui l’aproximacio actual del zero que volem calcular, i finalment un altredouble que es el valor que pren f(x) en aquest punt.

15

16 CAPITOL 3. ZEROS DE FUNCIONS

Capıtol 4

Zeros de Funcions

4.1 Zeros de funcions

Volem calcular els zeros d’una certa funcio f(x) dins un interval [a, b]. El procedimentque seguirem es, en primer lloc, separar els possibles zeros (considerant que la funcio siguicontınua) fent un escombrat de l’interval d’estudi i detectant possibles canvis de signe. Unavegada determinat el subinterval en el qual hi ha un zero, aplicarem algun dels metodes decalcul de zeros. En aquesta practica, el que farem es calcular per duplicat els zeros, perpoder fer un estudi comparatiu de les diferents velocitats de convergencia dels metodes deNewton i de la secant.

Exercici 4.1.1 Considerem la funcio f(x) = 2x − ln x − 4 dins de l’interval [0, 4]. Volemconeixer els seus zeros amb una precisio tol<1.e-12.

• Dibuixeu la grafica de la funcio f(x).

• Calculeu els seus zeros pels metodes de Newton i la secant. Si el canvi de signe corresponal subinterval [ak, bk], preneu aquests valors com a inicials en el cas de la secant i preneuak com a valor inicial en el cas de Newton.

Doneu els resultats en un fitxer de resultats que anomenarem zeros.out cada una de lesiteracions necessaries per a calcular el zero corresponent amb els dos metodes. Per uni-formitzar, a cada lınia podeu escriure tres valors: un valor int corresponent a la iteracio,un double que sigui l’aproximacio actual del zero que volem calcular, i finalment un altredouble que es el valor que pren f(x) en aquest punt.

17