El número de oro

Las proporciones de un rectángulo

Hasta hace poco eran casi universa-les los aparatos de TV cuyo formato de pantalla era 4:3. Esto significa que

3

4

pantalla la de Altura

pantalla la de Anchura

Las proporciones de un rectángulo

En la actualidad es posible elegir entre otros formatos, siendo frecuente el 16:9; incluso es posible elegir qué for-mato usar dependiendo de la emisión que se esté recibiendo.

El formato, independientemente del ta-maño del televisor, nos determina la forma del rectángulo que vemos.

Formato 4:3 Formato 16:9

Un problema geométrico

La figura que se da a continuación es un rectángulo dividido en un cuadra-do y otro rectángulo.

¿Qué formato del rectángulo inicial hacen que el segundo rectángulo sea semejante al primero?

¿El rectángulo mas armónico?

Si el lado del cuadrado lo tomamos igual a 1, y es x la medida del lado mayor del rectángulo, debe cumplirse que

1 -x

1

1

x

Resolviendo esta ecuación, que tiene dos soluciones, la única que tiene sentido es la positiva, y resulta ser:

.....46180339887.12

51

A este número se le llama “número áureo”, o número de oro, y se suele representar por la letra griega

Nótese que la ecuación que resuelve nuestro problema puede escribirse así:

1 -xx

1

11

Como el número es solución de esa ecuación resulta que

es decir

...6180339.01...6180339.1...6180339.1

1

El rectángulo de formato :1 fue considerado en la antigüedad clásica griega como el más estéticamente agradable, y hoy en día nuestro DNI, carnet de conducir y tarjetas bancarias responden con bastante exactitud a dicho formato.

En el Partenon se encuentran ejemplos de rectángulos que responden a la pro-porción áurea.

Desde el Renacimiento, muchos artistas, singularmente pintores, han utilizado en sus obras dimensiones relacionadas con la razón áurea.

Soneto de Rafael Alberti

A ti, maravillosa disciplina,media, extrema razón de la hermosuraque claramente acata la clausuraviva en la malla de tu ley divina.A ti, cárcel feliz de la retinaáurea sección, celeste cuadratura,misteriosa fontana de mesuraque el Universo armónico origina.A ti, mar de los sueños angulares,flor de las cinco formas regulares,dodecaedro azul, arco sonoro.Luces por alas un compás ardiente.Tu canto es una esfera transparente.A ti, divina proporción de oro.

Pero hay mucho más detrás del número áureo.

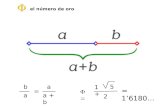
Notemos primero un hecho que puede parecer sorprendente.

Partimos de un rectángulo de altura a y anchura b arbitrarios, y por tanto de formato b:a

Tomemos, por ejemplo, a=3, b=11. Ahora construimos esta sucesión de números:

3, 11, 14, 25, 39, 64, 103, 167, 270,..

Como se ve, cada término a partir del tercero es suma de los dos que le preceden.

¿Cómo son los formatos de los rectán-gulos cuyos lados son dos términos consecutivos de la sucesión? Veamos:

FORMATO VALOR DECIMAL11:3 3,6667

14:11 1,2727

25:14 1,7857

39:25 1,5600

64:39 1,6410

103:64 1,6094

167:103 1,6214

270:167 1,6168

FORMATO VALOR DECIMAL

437:270 1.6185

707:437 1,6178

1144:707 1,6181

Si siguiéramos un poco más calculan-do términos de la sucesión veríamos la tendencia:

El cociente entre la anchura y la altura se va aproximando al número áureo.

Este hecho es cierto cualquiera que sea la elección de los dos primeros números, lo cual revela una conexión entre el número áureo y las sucesio-nes que obedecen a la regla de forma-ción antes expuesta.

La sucesión de Fibonacci

La más sencilla entre todas se obtiene cuando los dos primeros términos son iguales a 1:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…

Esta sucesión se conoce con el nombre de “sucesión de Fibonacci”

La sucesión de Fibonacci

Su interés se debe a que aparece en la naturaleza donde no esperaríamos encontrarla. Por ejemplo, en el caso de las pepitas del girasol, estas se disponen según espirales cuyo núme-ro es un término de la sucesión de Fibonacci.

La sucesión de Fibonacci

La sucesión de Fibonacci