Determine h y k de tal manera que el conjunto solucin del sistema (i) sea vaco, (ii) contenga una solucin nica y (iii) con

UNIVERSIDAD DE PIURA

FACULTAD DE INGENIERIA

CURSO: COMPLEMENTOS DE LGEBRA

PRACTICA N 5Viernes 7 de noviembre de 2008 Hora: 3:00 P.M.

Duracin: 2 h.

NOMBRE:...................................................................

SIN LIBROS, APUNTES, CALCULADORA, NI CUADERNILLO EXTRA

1. Sean: , , , , ,

a. Si , encuentre la dimensin y una base para H.(2 puntos)b. Si , encuentre la dimensin y una base para el espacio nulo de la matriz A.

(2 puntos)c. Determine si est en el espacio nulo de la matriz A.

(1 punto)d. Determine si est en H.

(1 punto)2. Sean:

, , ,

a. Encuentre una base para tal que P sea la matriz de cambio de coordenadas de a la base . (Sugerencia: Qu representan las columnas de P?(

(3 puntos)b. Encuentre una base para tal que P sea la matriz de cambio de coordenadas de a la base .

(2 puntos)3. En , encuentre la matriz de cambio de coordenadas de la base a la base cannica . Despus encuentre el vector coordenadas para .(2.5 puntos)4. Sea el conjunto de todas las matrices de la forma . Demuestre que: es una base de V.(2.5 puntos)5. Marque cada proposicin como verdadera o falsa. Justifique cada respuesta.a. Una base es un conjunto linealmente independiente lo ms grande posible.

b. El conjunto solucin de es un subespacio lineal.

c. Si B es cualquier forma escalonada de A, entonces las columnas pivote de B forman una base para el espacio columnas de A.

d. Si est en un espacio vectorial V, si es una base para V y contiene n vectores, entonces el vector coordenadas de est en .

Nota: - Slo se corregir las respuestas que hayan sido justificadas.

- Slo los enunciados falsos se pueden justificar con contraejemplos.

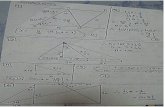
(1 punto c/u)SolucinPregunta 1.a) para encontrar la dimensin y una base para hallamos la forma escalonada de la matriz

( Forma Escalonada

Como la forma escalonada tiene 3 pivotes entonces la dimensin de H es 3, en realidad . Los vectores columna L.I son las columnas 1, 2 y 4. Por tanto una base para H es:

b) ; es la solucin de . Hallamos la solucin del sistema homogneo. Continuamos hallando la forma escalonada reducida:

Entonces: (

. Por tanto

La dimensin de es 1 y una base para seria

c) ; como , no est en .

d) est en H si se puede expresar como combinacin lineal de . Como generan entonces est en H.

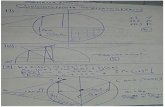
Pregunta 2.a) Sean las bases: y .

Como P es la matriz de cambio de coordenadas de la base U a la base V, entonces sus vectores columnas estn expresados en la base V y representan los vectores en base V . Por tanto P sera:

El vector est formado por los escalares en la combinacin lineal de los vectores para formar :

, es decir si , entonces:

, de igual manera:

Reemplazando:

Entonces la base U ser:

b) Tenemos que

Hallamos :

Entonces:

,

Reemplazando:

Por tanto

Pregunta 3.La matriz de cambio de coordenadas de la base B a la base cannica es formada por los vectores de la base B

El vector B-coordenadas para -1+2x est formado por los escalares de la combinacin lineal de los polinomios de B para obtener el polinomio -1+2x:

Usando el isomorfismo:

Por tanto

Pregunta 4.Tenemos que demostrar que las matrices de B son L.I. y genera V.

Las matrices son linealmente independientes si generan la matriz nula con unicidad. Usamos el isomorfismo vectorial:

Como la matriz tiene 1 pivote en cada columna entonces los vectores son L.I. por tanto las matrices son L.I.

Tenemos que demostrar que los vectores equivalentes de las matrices de B generan el subespacio V.

De donde los vectores generadores de V son las matrices equivalentes serian:

EMBED Equation.3 Por tanto la base para V es: ... demostrado.

Pregunta 5.a. Verdadero. Una base es un conjunto linealmente independiente lo ms grande posible porque cualquier vector del espacio correspondiente se puede expresar como combinacin lineal de los vectores de la base, por tanto si se agrega un vector ms al conjunto formado por los vectores de la base entonces ese nuevo conjunto ya ser linealmente dependiente.a. Verdadero. El conjunto solucin de es un subespacio lineal porque satisface las condiciones de un subespacio lineal, es decir si y son dos vectores del conjunto solucin de , entonces se cumple que y (c es un escalar) pertenecen al conjunto solucin de . Demostracin:

Si a la solucin de

Si a la solucin de

Para demostrar que pertenece al conjunto solucin de , tenemos que demostrar que

Usando las propiedades de la multiplicacin de matrices tenemos:

, entonces pertenece al conjunto solucin de .Por ltimo:

, entonces tambin pertenece al conjunto solucin de

b. Falso. Porque para formar una base para el espacio columnas de A debemos tomar las columnas linealmente independientes de A y no de B. Las columnas pivote de la forma escalonada B nos da la posicin en las que se encuentran las columnas de A linealmente independientes.c. Verdadero. Porque el vector coordenadas de est formado por los escalares de la combinacin lineal de los vectores de la Base para formar el vector y si tiene n vectores entonces van a existir n escalares en la combinacin lineal y por tanto el vector coordenadas de est en .

PAGE 1

_1287469470.unknown

_1287858262.unknown

_1287859709.unknown

_1287860788.unknown

_1287861540.unknown

_1287861642.unknown

_1287861839.unknown

_1288605205.unknown

_1288605177.unknown

_1287861838.unknown

_1287861579.unknown

_1287860949.unknown

_1287861177.unknown

_1287860806.unknown

_1287860200.unknown

_1287860458.unknown

_1287860775.unknown

_1287860267.unknown

_1287859782.unknown

_1287859885.unknown

_1287859772.unknown

_1287858861.unknown

_1287858935.unknown

_1287859179.unknown

_1287859490.unknown

_1287859690.unknown

_1287859308.unknown

_1287859074.unknown

_1287858910.unknown

_1287858921.unknown

_1287858764.unknown

_1287858842.unknown

_1287858780.unknown

_1287858625.unknown

_1287858641.unknown

_1287858342.unknown

_1287858352.unknown

_1287856439.unknown

_1287857163.unknown

_1287857448.unknown

_1287857641.unknown

_1287857356.unknown

_1287857088.unknown

_1287856552.unknown

_1287856599.unknown

_1287855806.unknown

_1287855906.unknown

_1287856280.unknown

_1287855859.unknown

_1287469572.unknown

_1287469610.unknown

_1287469557.unknown

_1273687588.unknown

_1287466647.unknown

_1287468156.unknown

_1287468916.unknown

_1287468960.unknown

_1287468995.unknown

_1287468177.unknown

_1287467553.unknown

_1287468129.unknown

_1287468138.unknown

_1287467468.unknown

_1287464610.unknown

_1287466615.unknown

_1287466631.unknown

_1287466597.unknown

_1287464628.unknown

_1273688049.unknown

_1287464554.unknown

_1287464580.unknown

_1273688948.unknown

_1287463842.unknown

_1273688107.unknown

_1273687729.unknown

_1273687768.unknown

_1273687711.unknown

_1273686689.unknown

_1273687196.unknown

_1273687292.unknown

_1273687479.unknown

_1273687226.unknown

_1273687007.unknown

_1273687120.unknown

_1273686802.unknown

_1273685185.unknown

_1273685289.unknown

_1273685360.unknown

_1273685462.unknown

_1273685634.unknown

_1273686669.unknown

_1273685822.unknown

_1273685530.unknown

_1273685415.unknown

_1273685454.unknown

_1273685248.unknown

_1273553029.unknown

_1273553240.unknown

_1273685166.unknown

_1273553075.unknown

_1273510488.unknown

_1273510496.unknown

_1273510370.unknown

_1273172690.unknown

_1273173313.unknown

_1273170081.unknown