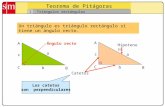
El Teorema de Pitágoras Establece Que en Todo Triángulo Rectángulo
-
Upload
jhonalexaderlopezmoreno -
Category
Documents
-
view
10 -
download
2
description
Transcript of El Teorema de Pitágoras Establece Que en Todo Triángulo Rectángulo
El teorema de Pitgoras establece que en todo tringulo rectngulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos .Teorema de PitgorasEn todo tringulo rectngulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Pitgoras
Si un tringulo rectngulo tiene catetos de longitudes y , y la medida de la hipotenusa es , se establece que:(1)De la ecuacin (1) se deducen fcilmente 3 corolarios de aplicacin prctica:
ndice[ocultar] 1 Historia 2 Designaciones convencionales 3 Demostraciones 3.1 China: el "Zhou Bi Suan Jing", y el "Jiu Zhang Suan Shu" 3.2 Demostraciones supuestas de Pitgoras 3.3 Demostracin de Euclides: proposicin I.47 de Los Elementos 3.4 Demostracin de Pappus 3.5 Demostracin de Bhaskara 3.6 Demostracin de Leonardo da Vinci 3.7 Demostracin de Garfield 4 Vase tambin 5 Notas 6 Bibliografa 7 Enlaces externosHistoria[editar]Respecto de los babilonios hay esta nota:Desde el punto de vista matemtico, las novedades ms importantes que registran los textos babilnicos re refieren a la solucin algebraica de ecuaciones lineales y cuadrticas, y el conocimiento del llamado "teorema de Pitgoras" y de sus consecuencias numricas.[1]El teorema de Pitgoras tiene este nombre porque su demostracin, sobre todo, es esfuerzo de la mstica escuela pitagrica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocan ternas de valores que se correspondan con los lados de un tringulo rectngulo, y se utilizaban para resolver problemas referentes a los citados tringulos, tal como se indica en algunas tablillas y papiros. Sin embargo, no ha perdurado ningn documento que exponga tericamente su relacin [citarequerida]. La pirmide de Kefrn, datada en el siglo XXVIa.C., fue la primera gran pirmide que se construy basndose en el llamado tringulo sagrado egipcio, de proporciones 3-4-5.Designaciones convencionales[editar]
Tringulos Resumen de convenciones de designacin
Vrtices
Lados (como segmento)
Lados (como longitud)
ngulos
Demostraciones[editar]El teorema de Pitgoras es de los que cuenta con un mayor nmero de demostraciones diferentes, utilizando mtodos muy diversos. Una de las causas de esto es que en la Edad Media se exiga una nueva demostracin del teorema para alcanzar el grado de "Magster matheseos".Algunos autores proponen hasta ms de mil demostraciones. Otros autores, como el matemtico estadounidense E. S. Loomis, catalog 367 pruebas diferentes en su libro de 1927 The Pythagorean Proposition.En ese mismo libro, Loomis clasificara las demostraciones en cuatro grandes grupos: las algebraicas, donde se relacionan los lados y segmentos del tringulo; geomtricas, en las que se realizan comparaciones de reas; dinmicas a travs de las propiedades de fuerza, masa; y las cuaterninicas, mediante el uso de vectores.China: el "Zhou Bi Suan Jing", y el "Jiu Zhang Suan Shu"[editar]
Prueba visual para un tringulo de a=3, b=4 y c=5 como se ve en el Chou Pei Suan Ching, 500-200a.C.
El "Zhou Bi" es una obra matemtica de datacin discutida en algunos lugares, aunque se acepta mayoritariamente que fue escrita entre el 500 y el 300 a. C. Se cree que Pitgoras no conoci esta obra. En cuanto al "Jiu Zhang" parece que es posterior, est fechado en torno al ao 250a.C.El "Zhou Bi" demuestra el teorema construyendo un cuadrado de lado (a+b) que se parte en cuatro tringulos de base a y altura b, y un cuadrado de lado c.DemostracinSea el tringulo rectngulo de catetos a y b e hipotenusa c. Se trata de demostrar que el rea del cuadrado de lado c es igual a la suma de las reas de los cuadrados de lado a y lado b. Es decir:
Si aadimos tres tringulos iguales al original dentro del cuadrado de lado c formando la figura mostrada en la imagen, obtenemos un cuadrado de menor tamao. Se puede observar que el cuadrado resultante tiene efectivamente un lado de b - a. Luego, el rea de este cuadrado menor puede expresarse de la siguiente manera:
Ya que .Es evidente que el rea del cuadrado de lado c es la suma del rea de los cuatro tringulos de altura a y base b que estn dentro de l ms el rea del cuadrado menor:
Con lo cual queda demostrado el teorema.Demostraciones supuestas de Pitgoras[editar]
Se cree que Pitgoras se bas en la semejanza de los tringulos ABC, AHC y BHC. La figura coloreada hace evidente el cumplimiento del teorema.Se estima que se demostr el teorema mediante semejanza de tringulos: sus lados homlogos son proporcionales.[2]Sea el tringulo ABC, rectngulo en C. El segmento CH es la altura relativa a la hipotenusa, en la que determina los segmentos a y b, proyecciones en ella de los catetos a y b, respectivamente.Los tringulos rectngulos ABC, AHC y BHC tienen sus tres bases iguales: todos tienen dos bases en comn, y los ngulos agudos son iguales bien por ser comunes, bien por tener sus lados perpendiculares. En consecuencia dichos tringulos son semejantes. De la semejanza entre ABC y AHC:y dos tringulos son semejantes si hay dos o ms ngulos congruentes.
De la semejanza entre ABC y BHC:
Los resultados obtenidos son el teorema del cateto. Sumando:
Pero , por lo que finalmente resulta:
La relacin entre las superficies de dos figuras semejantes es igual al cuadrado de su razn de semejanza. En esto pudo haberse basado Pitgoras para demostrar su teoremaPitgoras tambin pudo haber demostrado el teorema basndose en la relacin entre las superficies de figuras semejantes.Los tringulos PQR y PST son semejantes, de manera que:
siendo r la razn de semejanza entre dichos tringulos. Si ahora buscamos la relacin entre sus superficies:
obtenemos despus de simplificar que: